[A/B Test] 통계적 가설 검정과 p-value
이번 포스트에서는 통계학을 접해 본 사람이라면 누구나 한번쯤은 들어봤을 법한 p-value에 대해서 리뷰해보도록 하겠다.
P-value는 통계적 가설 검정에서 가장 핵심적인 역할을 맡고 있다고 해도 과언이 아니다. 흔히 그 값이 0.05보다 작으면 “실험이 유의하다” 정도로 공식처럼 암기하고 있는 경우가 많지만, 막상 개념적으로 그 의미를 설명하기에는 까다로울 수 있다. 실제로 예전에 통계학개론 수업을 들을 때 조부모님께 p-value를 설명하는 것이 과제로 나온적이 있었다..
그만큼 통계학 전공자들에게도 p-value를 명쾌하게 설명하기란 쉬운 일이 아닌데, 그 이유는 애시당초에 개념 자체가 직관적이지 않은 부분도 있고, 더불어 p-value를 제대로 설명하려면 통계학이 무엇을 하려는 학문인지에 대한 명확한 이해가 필요하기 때문이다.
이러한 측면에서 해당 포스트에서는 간단하게 통계학의 세계관을 훒어본 다음, p-value의 정확한 의미에 대해서 이야기해보도록 하겠다.
1. 과학의 발전과 통계학의 탄생
본격적인 이야기에 들어가기에 앞서, 간략하게 통계학이 탄생하게 된 배경에 대해서 살펴보자.
르네상스와 16세기의 종교 개혁 등을 거치면서, 인간의 사회는 점차 기존 신 중심의 세계관에서 논리성, 합리성이 강조되는 과학 중심의 세계관으로 변화하기 시작했다. 후세에 “과학 혁명” 이라고도 불리는 이 패러다임의 중심에는 우주 만물의 변하지 않는 “본질적인 진리“에 대한 호기심이 있었다. 예를 들어, 뉴턴과 같은 천문물리학자들은 행성들의 움직임이 복잡한 방정식으로 표현되는 정확한 공식에 의해 발생한다고 믿었고, 이를 밝혀내기 위해 상당한 노력을 기울였다. 이러한 측면에서 이를 결정론적 세계관이라고 부르기도 한다.

뉴턴의 중력의 법칙
하지만 그들의 노력에도 불구하고, 특정한 현상을 완벽하게 설명하는 공식은 찾을 수가 없었다. 모든 관측치들은 필연적으로 설명되지 않는 “불확실성 (오차)” 을 포함하고 있었으며, 당시의 과학자들은 그 이유가 망원경과 같은 측정 도구의 부정확함 때문이라고 생각했다.
시간이 흘러 물리학을 포함한 여러 과학의 분야에서 점점 더 정밀한 도구와 발전된 방법론이 등장했음에도 불구하고, 여전히 측정 대상에 대한 오차는 없어지지 않았다. 어떻게 하면 이러한 불확실성을 줄일 수 있을까 골머리를 앓던 와중, 사람들은 본질적인 의문을 제기하기 시작했다 - “어쩌면 모든 현상에 불확실성이 본질적으로 내재되어 있는 것은 아닐까?” 라는 생각을.
이러한 발상의 전환은 궁극적으로 통계학이라는 학문을 탄생시키는 계기가 되었다고 해도 과언이 아니다. 혹자는 이를 “통계적 혁명”이라고 부르기도 하는데, 그 아이디어를 좀 더 자세히 알아보도록 하자.
2. 통계학의 세계관
18세기까지의 과학을 지배하던 결정론적 세계관과는 반대로, 통계학은 ”카오스 이론” 을 바탕으로 하는 확률적인 세계관을 표방한다. 즉, 우리에게 관측되는 데이터는 여러 요인들의 복합적인 상호작용으로 인한 “오차”라는 불확실성을 포함한 값이라는 것이다.

결정론적 모형 vs 확률적 모형
그렇기 때문에 통계학에서는 관찰된 데이터 그 자체는 관심 대상이 아니게 된다. 이보다 더 중요한 것은 관찰된 데이터들을 발생시킨 “매커니즘” 이고, 통계학에서는 이를 “확률 분포” 로 정의하며 따라서 과학의 목표는 현상들에 내재된 확률 분포를 규명하는 것이 된다.
그렇다면 이렇게 내재된 확률 분포는 어떻게 밝혀낼 수 있을까? 통계학의 아버지라고 불리는 칼 피어슨 (Karl Pearson) 이 제시한 관점에 따르면, 모든 확률 분포는 “모수 (parameter)“라고 불리는 다음의 4가지 값들에 의해 정의된다.
-
평균 (mean): 산발적으로 흩어져 있는 측정 자료들의 중심
-
표준편차 (standard deviation): 측정 자료들이 평균을 중심으로 얼마나 멀리 있는지 정도
-
왜도 (symmetry): 측정 자료들이 평균을 기준으로 한쪽으로 쏠려있는 정도 (skewness)
-
첨도 (kurtosis): 드물게 발생하는 측정값들이 평균에서 얼마나 멀리 떨어져 있는지 정도 (tailedness)
이러한 프레임워크를 바탕으로 피어슨은 모든 데이터가 특정한 현상의 확률 분포에서 랜덤하게 발생되는 값이라고 생각했고, 그의 생각은 점차 과학을 지배하기 시작했다. 다시 말해, 관심 현상에 대한 확률 분포를 찾아내는 것, 즉 모수를 추정하는 것이 과학의 궁극적인 목표가 되기 시작했는데, 여기서 한가지 문제점은 모수의 참 값을 실제로 알 수가 없다는 점이다.
바로 이 지점이 통계학이라는 학문이 탄생하게 된 직접적인 계기이다. 통계학에서는 추정하고자 하는 모수에 대한 “그럴싸한” 값을 관측된 데이터 (표본) 를 바탕으로 제시하려는 것이 그 핵심적인 관심사라고 할 수 있다. 사실 현대 통계학에서 모수의 개념은 앞서 설명한 것보다 훨씬 확장되었으나, 그 본질적인 아이디어는 동일하다고 생각한다.
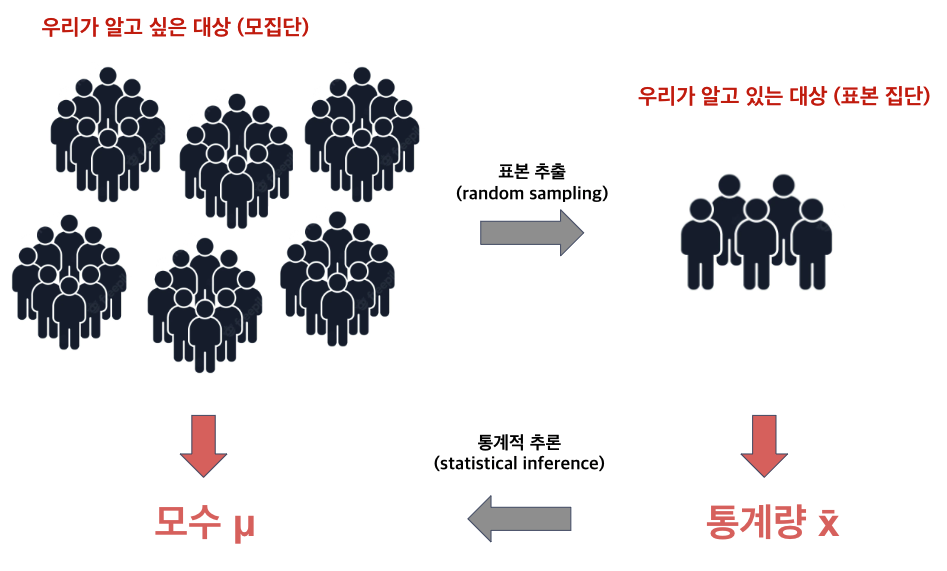
통계적 추론의 프레임워크
정리하자면, 우리에게 관측되는 모든 데이터는 모수들에 의해 정의되는 확률 분포로부터 랜덤하게 발생된다는 것이 지금까지의 핵심 내용이라고 할 수 있겠다. 편의상 통계학자들은 경험적으로 여러 현상들에서 자주 관측되는 분포들을 미리 정의해두었는데, 이를 표준 확률 분포라고 부르고 우리가 잘 아는 정규분포, 이항분포, 포아송분포 등이 대표적인 분포들이다.
이 과정에서 마치 유니콘과 같은 모수를 나름 합리적으로 추정하려는 시도가 통계학이며, 이 과정을 좀 더 세분화하면 다음과 같이 통계적 “추정”, “검정”, “예측“의 세가지 범주로 구분할 수 있다.
-
추정: 모수의 그럴싸한 값을 구하는 것
-
검정: 모수에 의한 어떠한 가설 (statement) 에 대해 의사결정을 내리는 것
-
예측: 모수로 인해 발생할 수 있는 미래의 값을 구하는 것
사족이지만, 해당 분류에서 세번째 “예측“에 특화된 학문이 바로 머신러닝과 딥러닝이다.
이제 본격적으로 p-value를 살펴보기 위한 준비가 끝났다. 이후 내용에서는 두번째 “검정“에 집중해서 p-value에 의미와 역할에 대해 구체적으로 살펴보도록 하겠다.
3. 통계적 가설 검정과 p-value
앞선 내용을 바탕으로 통계적 추론을 한마디로 정의하면 다음과 같다.
- “데이터라는 증거를 바탕으로 숨겨진 진실인 모수를 찾는 과정”
그 중에서도 통계적 “(가설) 검정”이란, 모수와 관련한 상반된 주장에 대해 관측된 데이터를 바탕으로 시시비비를 가리는 과정이라고 이해할 수 있다. 통계학의 언어를 빌리자면, 이 때 현상을 유지하려는 주장을 “귀무 가설”, 기존 현상을 반박하는 주장을 “대립 가설“이라고 표현한다.
이 과정은 종종 법정 재판에 비유되곤 한다. 통계적 검정의 절차에서 우리는 판사이다. 예를 들어, 어떠한 사람 A가 본인은 콜라와 펩시를 맛으로 구분할 수 있다는 주장을 했다고 가정해보자. 그리고 그의 이러한 주장에 대해서 사람들은 의심쩍은 눈초리로 “에이 설마 그게 가능하겠어?” 라고 미심쩍은 반응을 보였다. 해당 상황을 통계적 가설 검정의 프레임워크 아래에서 표현하자면, 귀무가설은 “A는 펩시와 콜라를 맛으로 구분할 수 있다” 이고 대립가설은 “A는 펩시와 콜라를 맛으로 구분할 수 없다” 가 된다.
이 때 한 가지 중요한 점은 가설 검정의 절차는 “무죄 추정의 원칙“을 따른다는 점이다. 즉, 기존의 주장이 틀리다는 것을 증명할 책임은 새로운 주장을 하는 측에 있으며, 충분한 “증거”가 없는 한 우리는 원래의 주장(귀무 가설)이 맞다는 것을 전제로 논의를 진행하게 된다. 앞선 예시를 다시 들자면, “A는 펩시와 콜라를 맛으로 구분할 수 있다”라는 주장이 틀리다는 것을 증명하기 위한 증거가 불충분하다면 해당 주장이 적어도 임시적으로는 맞다고 생각하는 것이다 (innocent until proven guilty).
그렇다면 구체적으로 귀무 가설을 어떻게 반박할 수 있을까? 통계적 가설 검정에서의 “증거”란 관측된 데이터를 의미한다. 직관적으로, 귀무가설이 맞다는 전제 아래에서 관측되기가 어려운 데이터들이 많이 모이면 모일수록 귀무 가설이 틀렸다는 주장을 내리기가 쉬워지는 것이 자연스럽다.

이의 있소 !! (Feat. 역전 재판)
이러한 A의 주장을 검정하기 위해 다음과 같은 실험이 진행되었다.
- A의 눈을 가리고, 무작위로 펩시와 콜라 중 하나를 맛보게 한 다음, 어떤 음료였는지를 맞추도록 하는 과정을 100번 반복
이 때, 우리의 관심 모수는 100번 중에 A의 평균적인 정답율이 몇퍼센트인지, 즉 “100번의 시행 중 A가 펩시와 콜라를 제대로 구분한 횟수의 비율” 이라고 정의할 수 있다. 앞서 모든 현상은 그만의 확률 분포를 따른다고 했던 것을 기억하자. 이러한 맥락에서 해당 예시에서 수집되는 데이터는 “성공” 또는 “실패”의 두가지 결과 중 하나가 관측되는 이항분포 (Binomial Distribution) 을 따른다고 할 수 있다.
만약 위 실험의 결과로 A가 100번 중 80~90번 정도 콜라와 펩시를 제대로 구분했다면, 이는 A가 정말로 두 음료를 잘 구분할 수 있다는 것을 입증하는 객관적인 증거라고 파악할 수 있다. 하지만 반대로 A의 정답률이 100번 중 20~30번이라면 그의 주장이 틀렸다고 판단하는 것이 자연스러울 것이다.
이러한 맥락에서 p-value란 수집된 증거들이 “귀무 가설에 반(反)하는 정도“를 구체적으로 수치화한 것이다. P-value의 기술적인 정의는 다음과 같다.
“the probability of obtaining a result at least as extreme as the results actually observed, under the assumption that the null hypothesis is correct” (wikipedia)
간단히 말해서, p-value는 귀무 가설이 맞다고 가정했을 경우에 주어진 데이터들이 발생할 확률을 의미하는 것이다.
앞선 실험의 결과로 p-value가 0.01이 나왔다고 가정하자. 이는 A의 주장이 맞다는 전제하에 실험의 결과가 관측될 확률이 겨우 1% 밖에 되지 않는다는 것을 의미한다. 이렇게 고작 1%의 확률로 발생할 수 있는 데이터들이 실제로 관측되었다는 사실은 우리로 하여금 귀무 가설 자체의 타당성에 대해서 의문을 품을 수 있는 객관적인 증거가 되는 것이고, 이를 바탕으로 우리는 “뭐야 A는 펩시랑 콜라를 제대로 구분하지 못하네..” 라고 당당히 이의를 제기할 수 있게 되는 것이다.
물론 정말 우연하게 1%의 확률로 해당 데이터들이 관측됐을 수도 있다. 이를 통계학에서는 1종 오류 (Type I error) 라고 부르는데, 통계적 가설 검정에서는 이러한 오류의 허용 한도 (유의수준) 를 사전에 지정해둔다. 따라서 일반적인 기준인 0.05의 유의 수준 아래에서 진행된 가설 검정 절차는, 우리가 가설 검정의 결과로 잘못된 결론을 내릴 확률을 딱 5%까지만 용납하겠다는 것을 의미한다.
정리하자면, 통계적 가설 검정은 실제로 관측된 데이터가 얼마나 “그럴싸한” 값인지를 귀무가설의 관점에서 “p-value”라는 값으로 수치화한 다음, 이를 바탕으로 의사결정을 내리는 과정이라고 이해할 수 있다.
다음으로는 p-value와 관련해서 몇가지 주의 사항에 대해 간단히 살펴보고 포스팅을 마치도록 하겠다.
4. p-value의 오해와 남용
🚨(1) P-value는 모수에 대한 확률이 아니다 !!
이는 왜 p-value가 직관적인 지표가 아닌지를 보여주는 부분인데, 실험의 결과로 구한 p-value를 모수에 대한 확률로 해석하는 것은 가장 흔한 실수 중 하나이다. 그 이유는 전통적인 통계학에서는 모수를 고정된 상수로 가정하기 때문인데, 상수는 어떤 특정한 값을 가질 확률이 100% 또는 0%이기 때문에 확률적인 해석 자체가 무의미하게 된다. (물론 베이지안 통계학에서는 예외이다. 이와 관련한 내용은 해당 포스트를 참고)
다시 한번 강조하자면, p-value의 정확한 정의는 “귀무가설이 맞다는 전제 아래 관측된 데이터들이 발생할 확률” 이다. P-value는 단순히 귀무가설이라는 틀 아래에서 정의된 것 일 뿐, 그 자체로 모수에 대한 확률적인 의미를 내포하지 않는다. 예를 들어, 앞선 예시에서 p-value가 0.05 라는 것을 “A가 콜라와 펩시를 제대로 구분할 확률이 5%이다” 라고 해석하는 것은 절대로 해선 안 될 실수이다!
🚨(2) 높은 p-value는 귀무가설이 옳다는 증거이다 ?
높은 p-value는 “대립가설을 입증하기 위한 증거가 불충분함” 을 의미한다. 앞서 통계적 가설 검정의 절차는 무죄 추정의 원칙 (innocent until proven guilty) 을 따른다고 했던 점을 기억하자. 이는 반대로 말하자면, 피고가 유죄인 것이 밝혀지지 않았다고 해서 피고가 실제로 죄를 저지르지 않은 것은 꼭 아니라는 점이다. 다만, 죄가 밝혀지지 않았기 때문에 “현 상황에서는 임시로 무죄로 간주하겠다”는 것일 뿐이다.
실제로도 대립가설이 옳고, 그 효과가 매우 강해도 데이터의 관측 숫자가 적으면 p-value가 높을 수 있는데, 그렇기 때문에 높은 p-value 는 “데이터 불충분” 정도로 이해하면 편하다. 통계적 가설 검정에서 귀무가설의 옳고 그름을 “증명”하는 것은 불가능하다. 말장난 같지만 이것이 전통적인 통계학의 규칙이다 (play by the rule!).
🚨(3) p-value가 낮다고 해서 결과가 실제로 유의미한 것만은 아니다 !
이게 무슨 소리냐고 생각할 수 있는데, 통계적 가설 검정으로 나온 결과를 해석할 때는 항상 “실용적 유의성“과 “통계적 유의성“을 잘 구분해야 한다.
예를 들어, “A라는 수면제가 평균 수면시간 증가에 도움이 된다” 라는 대립가설에 대한 검정을 진행한다고 해보자. 그 결과로 도출된 p-value가 0.0001 이라는 매우 낮은 값이라고 할 때, 이는 과연 수면제의 효과를 입증하는 것일까? 앞서 살펴본 가설 검정의 절차를 바탕으로 할 때 우리는 해당 수면제가 평균 수면시간 증가에 도움이 된다는 결론을 내릴 수는 있다 - “통계적으로는”.
하지만 만약 해당 약으로 인한 평균 수면시간 증가량이 1~2초 정도라면 이는 실질적으로는 전혀 의미가 없는 결과일 것이다. 이를 임상 통계학에서는 “임상적 유의성” 이라고 하는데, 두 집단간 평균의 차이를 검정하기 위해 흔히 사용되는 “two-sample t-test” 의 예시를 빌어 살펴보자면, 실제로 표본 크기가 굉장히 커지는 경우 두 집단간의 평균의 차이가 매우 작은 값이더라도 p-value는 굉장히 낮은 값이 나올 수 있다. 이처럼 표본 평균의 차이가 동일한 경우 관측치가 많아질 수록 p-value는 필연적으로 작아지는데, 이를 통계학에서는 가설검정의 “민감도 (sensitivity)” 라고 한다.
이렇듯 “통계적 유의성”이 “실용적 유의성”을 보장하는 것은 아니기 때문에 p-value를 너무 맹신하지 않는 것이 중요하다. 즉, p-value가 유의 수준보다 작다고 해서 장땡이 아니라는 점을 명심하자. 실제로 이와 관련해서 미국 통계학회는 p-value의 사용과 관련한 지침서까지 만들었을 정도인데, 제대로 이뤄진 연구에서는 실험의 유의성을 주장하기 위해 p-value와 신뢰구간을 함께 제시하는 경우가 일반적이다. (신뢰구간이 무엇인지에 대해서는 다음 포스트에서 다룰 예정이다.)