[A/B Test] 검정력
해당 포스트에서는 통계적 가설 검정에서 등장하는 “검정력“의 개념에 대해 리뷰해보도록 하겠다.
1. 가장 좋은 통계 검정 방법?
통계적 가설 검정이란 귀무가설과 대립가설이라는 상반된 두개의 가설을 세운 다음, 관측된 데이터를 이용해서 더 그럴싸 하다고 생각되는 한 개의 가설을 선택하는 절차이다. 그리고 이 과정에서 “더 그럴싸 함”을 판단하기 위한 객관적인 방법이 바로 통계 검정 방법 이라고 할 수 있다.
단, 이 과정에서 한가지 주의해야 할 점은 바로 하나의 통계 검정 문제 (ex. A/B Test) 에 대해 여러가지 통계 검정 방법들이 존재할 수 있다는 점이다. 가령, 서로 다른 두 그룹 A와 B의 평균을 비교하기 위한 방법에는 그 유명한 이표본 t검정 (two sample t-test) 이외에도 “윌콕슨 순위합 검정 (wilcoxon rank sum test)”, “크루스칼-왈리스 검정 (Kruskall-Wallis Test)” 등의 방법론들이 있다. 이러한 방법론들에 대한 자세한 정리는 해당 포스트를 참고하라.
그렇다면 왜 이처럼 하나의 문제에 대해 여러 가지 통계 검정 방법론들이 존재하는 것일까? 비유하자면, 마치 라면을 끓일 때 스프를 먼저 넣는 사람과 면을 먼저 넣는 사람이 있는 것처럼, 특정한 검정 문제에 대해 결론을 도출하는 방법 자체는 매우 다양할 수 있다. 극단적인 예로 “동전을 던져서 앞면이 나오면 A가 더 좋다고 결론 내리고, 뒷면이 나오면 B가 더 좋다고 결론 내리는 방법”이 있다고 해보자. 다소 황당하긴 하지만 이러한 방법 역시 의사 결정에 “일정한 기준”이 있다는 점에서 검정 방법이라고 할 수는 있다. 물론 이런 방법을 사용해서는 올바른 결과를 얻기가 힘들기 때문에 타당한 통계 검정 방법은 아닐 것이다.
이러한 맥락에서 통계 검정 방법의 “검정력”이란 여러 검정 방법론들을 비교할 수 있는 객관적인 성능 지표이다. 결론부터 말하자면, 가장 좋은 통계 검정 방법론이란 1종 오류를 유의수준 이하로 통제하면서, 검정력을 최대화하는 검정 방법 이다. 이를 이해하기 위해 필요한 통계적 개념들을 하나씩 파악해보도록 하자.
2. 1종 오류 vs 2종 오류
앞서 살펴본 것처럼 통계 검정 방법이란 주어진 데이터를 바탕으로 특정한 가설 검정 문제에 대한 결론을 내리기 위한 절차이다. 그리고 당연하게도 이렇게 도출된 결론은 맞을 수도 있고 틀릴 수도 있다. 카카오 프렌즈들을 빌려 다음의 두가지 경우를 생각해보자.
예시 1: 귀무가설이 실제로 “참”인 경우
-
귀무가설: 라이언은 사자이다. (참)
-
대립가설: 라이언은 사자가 아니다.
이 경우 우리가 세운 귀무가설은 실제로 참이기 때문에 가설 검정의 결과는 “귀무가설이 맞다” 라는 결론을 내려야한다. 하지만 혹자는 라이언의 귀여운 외형을 보고 곰이라고 잘못 판단해 귀무가설을 기각하고 대립가설을 채택할 수도 있다 (실제로 필자는 최근까지 곰인줄 알았다..) 이러한 상황을 통계학에서는 “1종 오류 (Type I error)“가 발생했다고 표현한다.
예시 2: 귀무가설이 실제로 “거짓”인 경우
-
귀무가설: 춘식이는 사자이다. (거짓)
-
대립가설: 춘식이는 사자가 아니다
예시 1과는 반대로, 이 경우는 실제로는 귀무가설이 거짓인 상황이다. 따라서 가설 검정의 결과로 “귀무가설이 틀리다”는 결론이 도출되어야 한다다. 하지만 위와 마찬가지로 어떤 사람은 춘식이가 라이언과 함께 살기 때문에 아기 사자일 것이라고 잘못 판단해서 귀무가설을 채택할 수도 있다. 이러한 상황을 통계학에서는 “2종 오류 (Type II error)“가 발생했다고 표현한다.

카카오프렌즈의 공식 소개
이렇듯 통계 검정 방법은 한번의 실험에 대해 “귀무가설이 맞다” 또는 “귀무가설이 틀리다” 중 하나의 결론을 제시하기 때문에, 이러한 검정을 여러번 반복했을 때 평균적으로 얼마나 제대로 된 결론을 내리는지가 중요한 관심사라고 할 수 있다. 이러한 맥락에서 1종 오류와 2종 오류의 개념은 상당히 중요하다.
1종 오류: 실제로는 귀무가설이 맞는데, 귀무가설이 틀렸다고 잘못 결론내릴 확률
- e.g. 예시 1에서 라이언이 사자가 아니라고 결론짓는 경우
2종 오류: 실제로는 귀무가설이 틀렸는데, 귀무가설이 맞다고 잘못 결론내릴 확률
- e.g. 예시 2 에서 춘식이가 사자라고 결론짓는 경우
한편, 일반적인 통계적 가설 검정에서 귀무가설은 현재 받아들여지고 있는 주장을 의미하며, 대립가설은 현재의 주장을 반박하는 주장 이라는 점을 저번 포스트에서 살펴본 바 있다. 이를 고려할 때, 귀무가설에 대한 기각은 현재의 주장을 뒤엎는 것이기 때문에 일반적으로 1종 오류가 2종 오류보다 훨씬 더 중요하게 고려된다.
그렇다면 1종 오류가 2종 오류보다 더 중요하니까 “1종 오류를 최소화하는 통계 검정 방법이 가장 좋은 것이 아닌가?” 하는 생각이 들 수 있다.
이를 반박하기 위해, 가령 수집된 데이터를 전혀 고려하지 않은채 “무조건 귀무가설이 맞다고 결론내리는 검정 방법“이 있다고 해보자. 이 경우 당연하게도 해당 검정 방법의 1종 오류는 정확하게 0% 이다. 왜냐하면 모든 결론이 귀무가설이 맞다고 주장하기 때문에, 귀무 가설이 틀렸다고 잘못 주장하는 경우는 없을 것이기 때문이다.
한편, 해당 방법의 치명적인 문제점은 귀무가설이 실제로 틀렸을 때 이를 틀렸다고 할 가능성이 전혀 없다는 점이다. 통계적으로 표현할 때, 이는 2종 오류가 100%인 상황입니다. 이렇듯 1종 오류와 2종 오류는 한쪽이 커지면 다른쪽은 작아지는 이른바 “tradeoff relationship“에 놓여있다 (그림 출처).
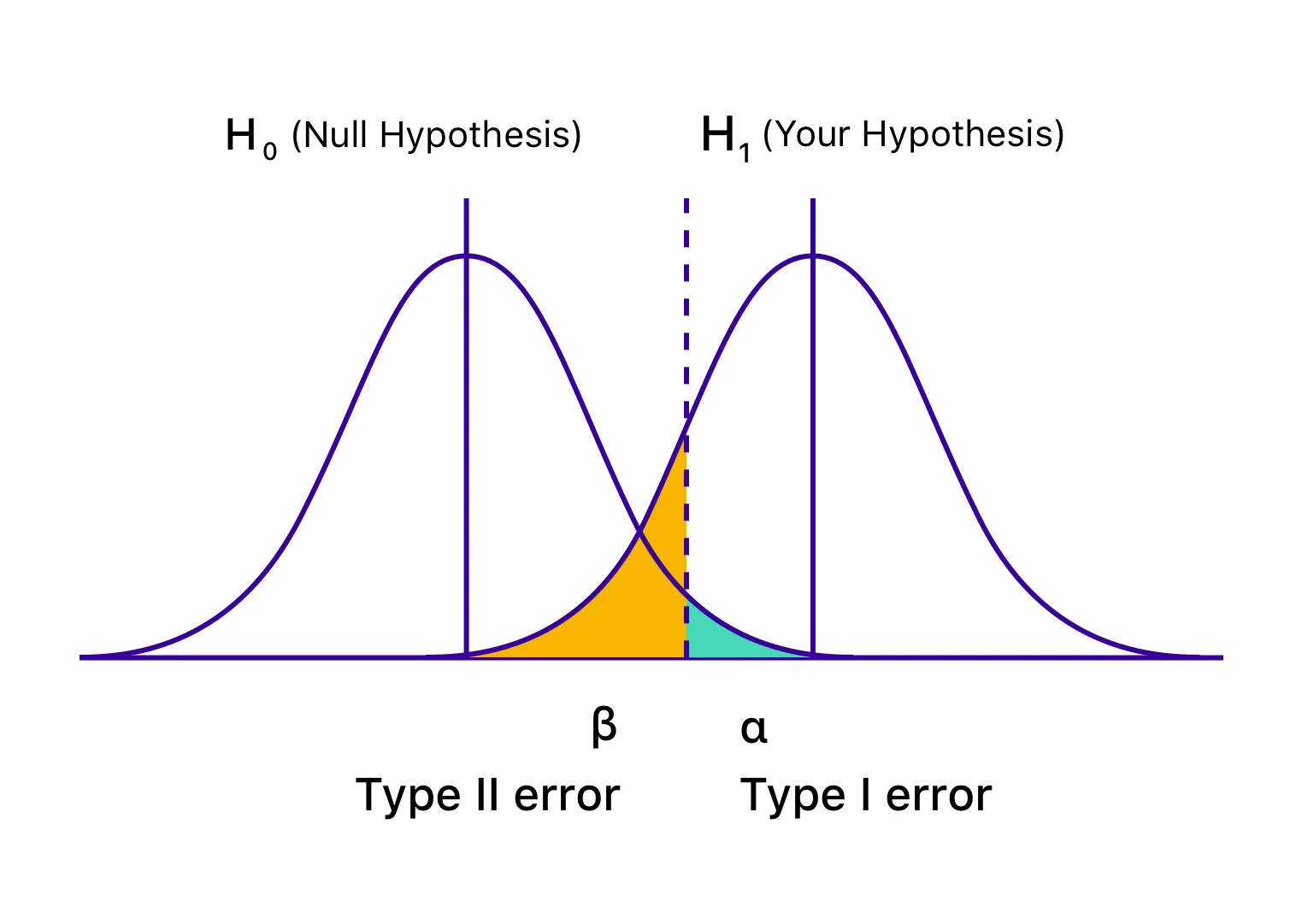
1종 오류와 2종 오류의 관계
그렇기 때문에 통계학자들은 이러한 두가지 오류 사이에서 적절한 타협점을 찾으려고 노력했고, 그 결과로 일반적으로 더 중요한 “1종 오류를 일정한 % 까지만 허용하자” 라는 합의에 다다랐다. 이러한 “1종 오류의 상한선”을 통계학에서는 흔히 그리스 문자 $\alpha$로 표현되는 “유의 수준 (significance level)” 이라는 용어로 나타내며, 우리에게 익숙한 0.05라는 기준이 일반적으로 사용된다.
따라서 어떠한 검정 방법이 통계적으로 타당하다고 인정받기 위한 최소한의 조건은 바로 1종 오류가 유의 수준 이하인 것이 이론적으로 보장되는지의 여부가 된다. 앞선 예시처럼 단순히 동전던지기를 통해 의사결정을 내리는 방법은 이러한 맥락에서 통계적으로 타당한 검정 방법이 아니라고 할 수 있다.
3. 검정력의 정의
앞선 내용에서 통계 검정 방법이란 1종 오류를 유의수준 이하로 컨트롤하는 의사 결정 방법이라는 점을 살펴보았다. 따라서 우리가 앞으로 고려할 모든 “타당한” 통계 검정 방법론에서 1종 오류는 더 이상 문제가 되지 않는다. (물론 한 번에 여러개의 가설 검정을 동시에 진행하는 경우 다중 검정 이라는 문제가 발생하긴 하지만, 이는 이후 포스트에서 자세히 다룰 예정이므로 여기서는 단 두 개의 가설만을 검정하는 상황을 바탕으로 논의를 진행하겠다.)
이러한 맥락에서, 우리의 자연스러운 다음 관심사는 “과연 2종 오류는 얼마일 것인가?” 이다. 바로 이 부분에서 해당 포스트의 주제인 검정력의 개념이 등장한다.
검정력 (statistical power) 이란, 2종 오류의 역 (逆, coverse) 사건에 대한 확률을 의미한다. 즉 검정력이란 “귀무가설이 틀렸을 때, 실제로 귀무가설이 틀렸다고 올바르게 결론을 내릴 확률“로 정의되며, 앞선 예시 2에서 춘식이가 사자가 아니라고 제대로 판단한 경우가 이에 해당된다. 참고로 통계학에서 2종 오류는 흔히 그리스 문자 베타(β)로 표현되며, 검정력은 (1-β) 로 정의된다. 이러한 상황 속에서 우리의 목표는 검정력이 가장 높은 가설 검정 방법을 찾으려는 것이다.
이렇게 가장 이상적인 검정 방법을 통계학에서는 “UMP (Uniformly Most Powerful) Test“라고 정의한다. 단, 문제는 UMP Test는 대부분의 가설 검정 문제에 대해 존재하지 않는다는 점이다. 좀 더 정확하게 말하면, 존재는 할 수 있으나 수식적으로 계산이 불가능하기 때문에 실제로 정의할 수 없는 것이다. 이와 관련해서 양측검정 문제에 대해서는 UMP Test가 존재하지 않는다는 것이 일반적으로 알려진 사실이다.
따라서 실제 가설 검정 절차는 “쉽게 사용할 수 있는” 여러가지 통계 검정 방법론 중에 가장 좋은 방법을 선택하는 방식으로 이루어진다. 여기에서 “가장 좋은 방법”이란 1종 오류를 유의 수준 이하로 제한하면서 검정력이 (그 중에서) 가장 높은 방법이 되는 것이다. 두 모평균에 대한 A/B Test에서 일반적으로 이표본 t검정이 사용되는 것이 바로 이 이유이다.
4. 검정력에 영향을 미치는 요인들
마지막으로, 일반적인 상황에서 통계 가설 검정 방법의 검정력에 영향을 미치는 몇가지 주요 요인들에 대해 살펴본 다음 포스트를 마무리하려고 한다. 구체적으로는, 이표본 t검정의 프레임워크 아래에서 논의를 진행해보겠다 (당연히 다른 사례에도 비슷하게 적용된다).
사실 통계 방법론의 검정력은 A/B Test의 기획 단계에서 굉장히 중요하게 고려되는 이슈이다. 그 이유는 검정력의 의미를 조금 생각해보면 알 수 있는데, 검정력이 낮은 검정 방법을 사용한다면 실제로 검증하고자 하는 효과가 유의미함에도 불구하고 이를 발견하지 못하게 된다. 즉, 어떠한 프로젝트가 단순히 “효과 없음”으로 결론나서 들어간 비용과 노력이 물거품이 될 수 있는 상황이 발생할 수 있기 때문에, 실험의 담당자는 사용될 검정 방법의 틀 아래에서 가능한 검정력을 최대로 높이기 위해 심혈을 기울이게 된다. 왜냐하면 대부분의 경우 결과의 유의미성을 것을 찾아내는 것이 A/B Test의 일차적인 목표이기 때문이다.
그렇다면 구체적으로 검정력은 어떻게 높일 수 있을까? 이를 수식적으로 확인해보기 위해 일반적인 이표본 t검정 (two sample t-test) 에서 표본 크기를 구하는 공식에 대해 살펴보도록 하겠다.
- 위 식에서 $n$은 표본크기, $\sigma^2$는 평가 변수의 모분산, $\alpha, \beta$는 각각 1종 오류와 2종 오류, 그리고 $\Delta$는 검정하고자 하는 효과의 크기 (i.e. effect size) 를 의미한다.
정리하자면, 검정력은 크게 다음의 세가지 요인의 영향을 받는다고 할 수 있다.
>> 1. sample size
>> 2. effect size
>> 3. 평가변수의 모분산
구체적으로, 검정력은 표본의 크기와 effect size에 비례하고 평가변수의 모분산에 반비례하며, 이를 바탕으로 우리는 검정력을 높이기 위해서 2종 오류, 즉 β를 최소화하고 싶은 상황이다.
이렇게 수식적으로만 살펴보면 직관적인 이해가 어렵기 때문에 구체적인 예시를 바탕으로 각 요인들이 어떻게 작용하는지를 파악해보도록 하겠다. 어떠한 두 농구선수 A와 B가 있다고 해보자. 그리고 우리는 두 농구선수의 “자유투 성공률”을 바탕으로 둘 중 어떤 선수가 더 자유투를 잘 던지는지를 검증해보고 싶은 상황이라고 가정하겠다.
이 상황에서, 우선 표본 크기란 두 선수가 각각 던진 자유투의 개수를 의미한다. 예를 들어, 첫번째 실험에서는 두 선수가 각각 자유투를 10번씩 던져서, 그 중에서 A는 8번, B는 7번 성공했다고 해보자. 반면 두번째 실험에서는 두 선수가 각각 자유투를 100번씩 던져서 A는 80번, B는 70번을 성공했다. 이 경우, 검증하고자 하는 평가지표, 즉 자유투 성공률의 차이는 10%로 첫번째 실험과 두번째 실험이 동일하다. 하지만 각각 10번의 자유투를 던져서 얻은 결과와, 각각 100번의 자유투를 던져서 얻은 결과 중 어떤 것이 더 신뢰할만한 결과라고 할 수 있을까? 당연하게도 시행 횟수가 더 많은 두번째 실험의 결과가 좀 더 믿을만 할 것이다. 왜냐하면 10번 시행에서는 단순히 우연에 의해 선수 B가 A보다 성공률이 높은 상황이 발생할 수 있기 때문이다. 따라서 표본의 크기가 증가하면 증가할 수록 두 선수의 자유투 실력을 더 정확하게 검증할 수 있게 되며, 검정력이 높아진다.
다음으로, effect size란 두 선수의 실제 자유투 성공률과 관련이 있는 개념이다. 물론 자유투 성공률을 실제로 알 수는 없지만 여기에서는 설명의 편의를 위해 알고 있다고 가정한다. 구체적으로, A와 B의 자유투 성공률이 각각 80%, 70%인 경우와 A와 B의 자유투 성공률이 각각 71%, 70%인 경우를 생각해보자. 이 경우, 첫번째 상황에서는 두 선수의 자유투 성공률 차이가 약 10% 인 반면, 두번째 경우에서는 겨우 1% 밖에 되지 않는다. 따라서 결과적으로 동일한 환경이더라도 첫번째 경우보다 두번째 경우에서 A가 B보다 더 자유투를 잘 쏜다라는 가설을 검정하기가 더 어려워지게 되는 것이다. 가령, 전자에서는 약 100번의 시행만으로 충분했다면, 후자는 자유투를 500번 던져도 1%의 차이를 발견해내기가 어려울 수 있다.
마지막으로 평가변수의 모분산은 각 선수의 자유투 실력의 기복과 관련이 있다. 예를 들어, 선수 A는 기복이 없이 꾸준하게 70% 정도의 성공률을 보이는 반면, 선수 B는 컨디션에 따라 좋을 때는 90%, 나쁠 때는 50% 까지 자유투 성공률의 차이가 발생한다고 해보자. 이렇게 평가 시점에 따라 지표의 값이 변동이 큰 선수 B의 경우 실험의 유의성을 주장하기가 어려워지게 된다. 즉, 평가변수의 모분산이 커질수록 검정력은 감소하는 반비례 관계가 성립하는 것이다.
위 내용을 종합하자면, 일반적으로 A/B Test를 설계하는 과정에서 이론적으로 대략 80% 정도의 검정력을 가질 수 있도록 앞서 말한 세가지 요인들을 조정한다. 단, 현실적으로 effect size를 바꿔가며 실험을 하는 것은 이상하기 때문에 검정력을 높이기 위해서 가장 쉽고 흔하게 사용되는 전략은 표본의 크기, 즉 실험의 진행 기간을 늘리는 것이다.
한편, 더 큰 표본을 수집하기 위해서는 추가적인 비용이 들어가게 된다. 이러한 맥락에서 평가 지표의 분산을 줄이는 것 역시 상당히 효과적인 경우가 많다. 단 이는 다소 까다로운 통계적 방법론들을 기반으로 하기 때문에, 통계학 전공자가 아닌 경우 쉽게 접근하기가 어렵다는 단점이 있다. 대표적으로는 마이크로소프트에서 제안한 CUPED 라는 기법이 있다. 이와 관련해서는 추후 기회가 되면 다뤄보도록 하겠다.