[MathStat] 4. Statistical Estimation

2022, Apr 24

This post is an overall summary of Chapter 7 of the textbook Statistical Inference by Casella and Berger.

Table of Contents

4.1 Overview

• Point Estimation
• Confidence Sets

4.2 Methods of Estimation

• Method of Moments (MoM) Estimators
• Maximum Likelihood Estimators (MLE)
• Properties of MLE
  • Invariance property
  • Consistency
  • Asymptotic Normality (w/ Fisher Information)
• Bayes Estimators

4.3 Evaluating Estimators

• Loss function and risk
• Admissibility
• Minimax Risk
• Bayes Risk

4.4 Strategies to find Minimax Estimators

• Bounding the Minimax Risk
• Least Favorable Prior

4.5 Nonparametric Estimation

• Estimation of Cumulative Distribution Functions (CDF)
• Estimation of Statistical Functionals (Plug-in estimators)
• Estimation of regression functions

4.6 Consistency in Nonparametric Bootstrap

• The Kolmogorov metric and consistency
• Example: the sample mean
• Failure of bootstrap

 

---

4. Statistical Estimation

Statistical estimation is the very procedure of an endeavor to understand various aspects of an underlying population based on collected samples, so it can naturally be regarded as the core of statistics.

But typically, we can’t afford to have lot of samples (at least those which are “meaningful”), so we need a statistical model that best reveals our understanding of the underlying distribution. In this sense, a statistical model is the set of all possible distributions F for a specific event of our interest. Broadly, we have two kinds of statistical models - “parametric” and “non”-parametric models.

In a parametric model, the set of possible distributions F can be described by a finite number of parameters. A canonical example is the Gaussian model with the location $\mu$ and scale parameter $\sigma$ which can be represented as:

$$ \begin{aligned} F = \Big\{ f(x;\mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}\text{exp}\Big(-\frac{(x-\mu)^2}{2\sigma^2} \Big), \quad \mu \in \mathbb{R}, \sigma > 0 \Big\} \end{aligned} $$

On the other hand, the non-parametric model is one in which $F$ cannot be parameterized by a finite number of parameters. The density estimation task is one of the popular examples.

 

---

4.1 Overview

 

4.1.1. Point Estimation

First of all, we focus our attention to the point estimation where we are dealing with a single “best guess” from the possible values of an unknown quantity of interest. Here, the quantity of interest is often called as the parameter which we often denote as $\hat\theta$ or $\hat\theta_n$.

So basically, a point estimator is a function of the random variables $X_1, \dots, X_n$ such that

$$ \hat\theta_n = g(X_1, \dots, X_n) $$

which makes $\hat\theta_n$ itself another random variable.

Because any function of the collected samples can be regarded as an estimator (it is easy to think of estimator as some kind of decision rule), we need some criteria to measure the performance of the many possible estimators and possibly define the best one. This was studied intensively in the field of mathematical statistics in the early 20th century, and most fundamental criteria include unbiasedness and consistency.

The bias of an estimator $\hat\theta$ is defined as:

$$ b(\hat\theta) = \mathbb{E}_\theta \big[\hat\theta\big] - \theta $$

So basically, the implication of an “unbiasedness” is that the expectation of an estimator is exactly the same as the true parameter.

On the other hand, we call that an estimator is “consistent” if the estimator converges to the true parameter in probability such that:

$$ \text{for any }\epsilon>0,\quad \mathbb{P}_\theta \big(|\hat\theta_n - \theta| \geq \epsilon\big) \to 0 \quad \text{as } n \to \infty $$

So by the definition, It is no doubt that these two criteria are the very least conditions to be satisfied for an estimator to be statistically valid.

Then for the class of estimators that passes the above two guardrail properties, the performance of an estimator is often measured by its variance, which is given by:

$$ \text{Var}_\theta[\hat\theta] = \mathbb{E}_\theta\big[(\hat\theta_n - \mathbb{E}_\theta[\hat\theta])^2\big] $$

In this sense, the “best” estimator is the one that achieves the minimum variance, and the existance of such best estimator (a.k.a. MVUE) for various statistics have been studied intensively in the field of mathematical statistics.

 

4.1.2. Confidence Sets

Remember that (classic) statistical inference consists of estimation and hypothesis testing, where in the latter a confidence set used to for decision making.

Specifically in general, we define a $1-\alpha$ confidence set $C_n$ for a parameter $\theta$ to be any set which has the property such that:

$$ P_\theta(\theta \in C_n) \geq 1-\alpha $$

where the left term $P_\theta(\theta \in C_n)$ is called as the coverage of the confidence set $C_n$. Intuitively, the implication of the coverage is that when an experiment is repeated sufficiently many times, then for every distinct confidence sets in different trials of experiments, the true parameter $\theta$ will be included in approximately $1-\alpha$ of those sets. This naturally connects to the definition of confidence intervals in a statistical testing procedure.

Actually, we can use concentration inequalities to construct confidence intervals. However, these confidence intervals are often too loose to have practical meanings so we often resort to asymptotic properties.

As an example, let’s consider a Bernoulli confidence set.

For Bernoulli random variables $X_1, \dots, X_n \overset{i.i.d}{\sim} Bernoulli(p)$, the Hoeffding’s inequality assures:

$$ P\big(|\hat p - p| \geq t \big) \leq 2e^{-2nt^2} = \alpha $$

By solving above inequality for $t$, it is straightforward that the confidence set is defined as:

$$ C_n = \Big( \hat p - \sqrt{\frac{log(2/\alpha)}{2n}}, \; \hat p + \sqrt{\frac{log(2/\alpha)}{2n}} \Big) $$

On the other hand, let’s see what happens when we use the normal approximation. By the asymptotic nomality of the Binomial random variables, we have the following (asymptotic) confidence interval:

$$ C_n = \Big( \hat p - z_{\alpha/2}\sqrt{\frac{\hat p (1-\hat p)}{n}}, \; \hat p + z_{\alpha/2}\sqrt{\frac{\hat p (1-\hat p)}{n}} \Big) $$

Then, by comparing the two confidence intervals, we know that the latter is always shorter than the interval obtained by Hoeffding’s inequality as long as the asymptoticity is valid.

$$ \Rightarrow z_{\alpha/2}\sqrt{\frac{\hat p (1-\hat p)}{n}} \leq \sqrt{\frac{log(2/\alpha)}{2n}} $$

 

---

4.2 Method of Estimation

Now let’s dive deeper into the methodogies of statistical estimation.

In this section, we are going to take a look at the three classes of estimation methods:

• Method of Moments (MoM) Estimator
• Maximum Likelihood Estimator (MLE)
• Bayes Estimator

Basically, all of these different methods are devised to estimate the parameters of our assumed statistical model. To this end, one might have the following questions:

• what happens if the model is wrong in the first place?
• where do models really come from?

Except for some rare cases when we have enough knowledge from our data to hypothesize a reasonable statistical model, the famous aphorism from George Box is always helpful as to not fall in a logical trap.

 

That is, when we specify a statistical model, we do so hoping that it can provide a useful approximation to the data generation mechanism. In this sense, as long as our model can provide us some useful insight about the underlying population, there is no right or wrong and the model is regarded as valid.

With this in mind, let’s firstly take a look at the Method of Moments Estimators.

 

4.2.1. Method of Moments (MoM) Estimators

Broadly, the idea of MoM estimators is to compare the estimated moments with the true (population) moments.

First of all, the sample moments are defined in a straightforward way such that:

$$ \begin{aligned} &m_1 = E[X] = \frac{1}{n} \sum_{i=1}^n X_i \\[10pt] &m_2 = E[X^2] = \frac{1}{n} \sum_{i=1}^n X_i^2 \\[10pt] &\quad\vdots \\[10pt] &m_k = E[X^k] = \frac{1}{n}\sum_{i=1}^n X_i^k \end{aligned} $$

Furthermore, let the i-th population moment be denoted as $\mu_i(\theta_1, \dots, \theta_k)$.

Then we can solve the following system of equations to derive the MoM estimators $\hat \theta_1, \dots, \hat \theta_k$:

$$ \begin{aligned} &\mu_1 = \mu_1(\theta_1, \dots, \theta_k) \\[10pt] &\quad\vdots \\[10pt] &\mu_k = \mu_k(\theta_1, \dots, \theta_k) \end{aligned} $$

To get a glimpse of what’s happening here, let’s take a look some examples.

 

<Example 1>

For a Gaussian random variables $X_1, \dots, X_n \sim N(\theta, \sigma^2)$, the MoM estimator is derived by solving:

$$ \begin{aligned} \mathbb{E}[X] &= \frac{1}{n}\sum_{i=1}^n X_i = \theta \\[10pt] \text{Var}(X) + (\mathbb{E}[X])^2 &=\frac{1}{n}\sum_{i=1}^n X_i^2 = \theta^2 + \sigma^2 \end{aligned} $$

As we have two unknown variables $\theta, \sigma^2$ and two independent equations, we can solve the equations to get the following MoM estimators:

$$ \begin{aligned} \hat\theta &= \frac{1}{n}\sum_{i=1}^n X_i \\[20pt] \hat \sigma^2 &= \frac{1}{n}\sum_{i=1}^n X_i^2 - \Big(\frac{1}{n}\sum_{i=1}^n X_i\Big)^2 \\[5pt] &= \frac{1}{n} \sum_{i=1}^n \Big(X_i - \frac{1}{n}\sum_{j=1}^n X_j \Big)^2 \\[10pt] &\Rightarrow \mathbb{E}[\hat\sigma^2] = \frac{n-1}{n} \sigma^2 \end{aligned} $$

From the result, we can see that the MoM estimators can naturally be biased.

 

<Example 2>

For a Binomial random variables $X_1, \dots, X_n \sim B(k, p)$, the MoM estimator can similarly be derived by solving:

$$ \begin{aligned} \mu_1 &= \mathbb{E}[X] = \bar X = kp \\[10pt] \mu_2 &= \mathbb{E}[X^2] = \frac{1}{n}\sum_{i=1}^n X_i^2 = kp(1-p) + k^2p^2 \end{aligned} $$

In this case, we don’t have a-priori “obvious” estimators for the parameter $k$ and $p$ because there can be multiple solutions to the above equation. Anyhow, one possible solution is:

$$ \begin{aligned} \hat p &= \frac{\bar X - \frac{1}{n}\sum_{i=1}^n(X_i - \bar X)^2}{\bar X} \\[15pt] \hat k &= \frac{\bar X^2}{\bar X - \frac{1}{n} \sum_{i=1}^n (X_i - \bar X)^2 } \end{aligned} $$

However, from the result we can see that the estimator for parameter $p$ is not confined in the original parameter space (i.e. $p \in [0,1]$). This can be problematic and one possible remedy is by truncating the estimator.

 

4.2.2. Maximum Likelihood Estimators (MLE)

So we have seen that the previous MoM estimators can become inefficient for some problems (i.e. example 2).

Supposedly most-commonly used method of defining an statistical estimator is from the likelihood function. Specifically, we want an estimator which maximizes the value of the likelihood function $L$ and denote it as the maximum likelihood estimator $\hat \theta_{MLE}$.

$$ \hat \theta_{MLE} = \underset{\theta}{\text{argmax}} \; L(\theta | X_1, \dots, X_n) $$

Intuitively, the MLE is just the value of the parameter which is most likely to have generated the samples, so using MLE as a surrogate for the parameter seems very natural.

Moreover, unlike the MoM estimators, MLE is always confined in the original parameter space (i.e. the support of MLE is the same as that of the parameter) and it has some desirable asymptotic properties which facilitates its use in many practical scenarios. In fact, much of the early theoretical development in statistics revolved around showing the optimality of MLE in various senses.

The canonical way of computing the MLE is to either analytically or numerically solve the following system of equations:

$$ \begin{aligned} &\frac{\partial}{\partial \theta_i} L(\theta | X_1, \dots, X_n) \overset{set}{\equiv} 0, \quad i = 1,\dots, k \\[10pt] &\Leftrightarrow \frac{\partial}{\partial \theta_i} \text{log}L(\theta | X_1, \dots, X_n) \overset{set}{\equiv} 0 \end{aligned} $$

, where logarithm of the original likelihood function is often taken for mathematical convenience.

 

<Example>

Apart from the trivial Gaussian and Binomial examples, let’s see the case where the MLE is not derived analytically.

Suppose $X_1, \dots, X_n$ are i.i.d. uniform random variables from a distribution with density:

$$ \begin{aligned} f(x;\theta) = \begin{cases} \frac{1}{\theta}, & \mbox{if } 0 \leq x < \theta \;\text{ and }\; \theta > 0 \\[10pt] 0, & \mbox{otherwise} \end{cases} \end{aligned} $$

Then, the likelihood function is given by:

$$ \begin{aligned} L(\theta | X_1, \dots, X_n) = \prod_{i=1}^n \frac{1}{\theta}\mathbb{1}\Big(0 \leq X_i < \theta \Big) = \frac{1}{\theta^n}\mathbb{1}\Big(0 \leq \underset{1\leq i\leq n}{\text{min}} X_i \Big) \; \mathbb{1}\Big(\underset{1\leq i\leq n}{\text{max}}X_i \leq \theta \Big) \end{aligned} $$

If we visualize this likelihood function, it would be something like:

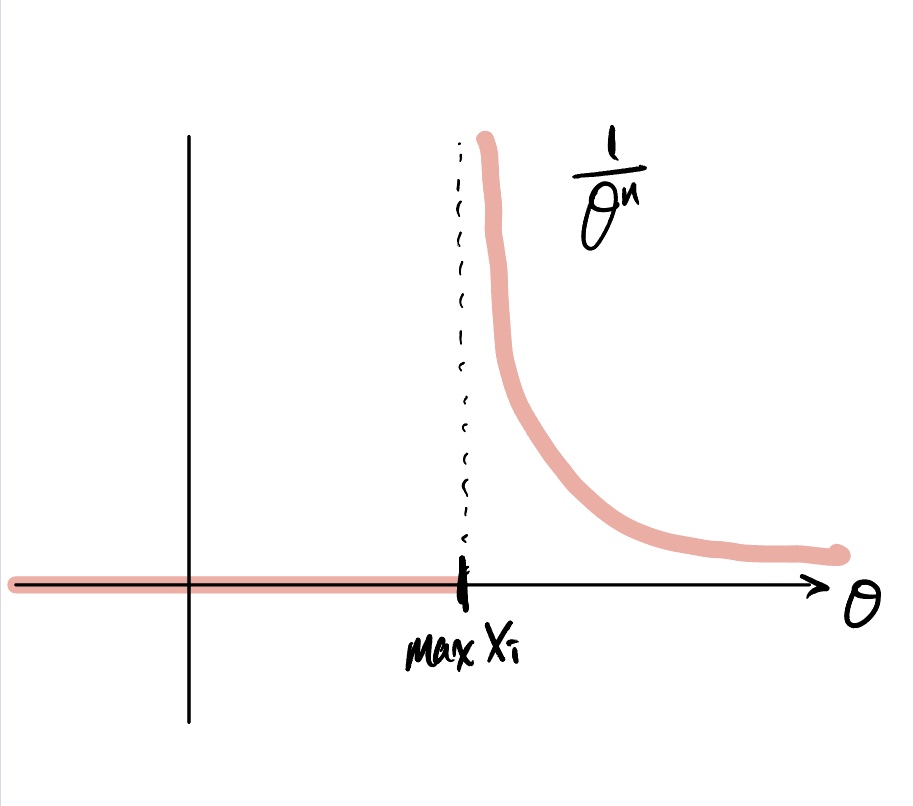
Therefore the MLE is:

$$ \hat \theta_{MLE} = \underset{1\leq i \leq n}{\text{max}}X_i $$

 

4.2.3. Properties of MLE

Now let’s quickly take a look at some of the desirable properties of the maximum likelihood estimators.

Note that many of the optimal properties are held under the so-called “regularity conditions”, and a brief introduction to some of the key conditions are:

• parameter space is closed and bounded
• true parameter lies within (interior of) the parameter space
• likelihood function is smooth (countably differentiable)

Also, as the MLEs cannot be derived analytically for most of the practical scenarios, we usually have to rely on numerical approximation techniques such as the Newton-Rhapson method or the gradient descent algorithm.

 

Invariance property

The first property of MLE we are going to look at is the invariance property. Roughly, what this states is that for a MLE $\hat \theta$ of a parameter $\theta$, the MLE for a function of the parameter $g(\theta)$ is just $g(\hat\theta)$.

A formal proof is (reference):

$$ \begin{aligned} &\text{Define }\Omega_\gamma = \{ \theta:g(\theta) = \gamma \}, \\[10pt] &\text{let } M_x(\gamma) = \underset{\theta \in \Omega_\gamma}{\text{sup}} L_x(\theta) \quad \text{(likelihood function induced by }g) \\[10pt] &\text{Our goal is to find }\hat\gamma \text{ at which } M_x(\gamma) \text{ is maximized}. \end{aligned} $$ $$ \begin{aligned} &\text{let } M_x(\hat \gamma_0) = \underset{\theta \in \Omega_{\hat\gamma_0}}{\text{sup}} L_x(\theta) \geq \underset{\theta \in \Omega_{\hat \gamma_0}}{L_x(\hat\theta)}, \quad \Omega_{\hat \gamma_0} = \{ \theta: g(\theta) = \hat \gamma_0 \} \end{aligned} $$ $$ \begin{aligned} \Rightarrow M_x(\hat\gamma_0) \leq \underset{\hat\gamma \in \Gamma}{\text{sup}} M_x(\hat \gamma) &= \underset{\hat\gamma \in \Omega}{\text{sup}} \; \underset{\theta \in \Omega_{\hat\gamma_0}}{\text{sup}} L_x(\theta) \\[10pt] &= \underset{\theta \in \Omega}{\text{sup}} L_x(\theta) = L_x(\hat \theta) \\[10pt] \Leftrightarrow M_x(\hat \gamma_0) = L_x(\hat \theta) &= \underset{\gamma \in \Gamma}{\text{sup}} M_x(\gamma) \\[10pt] \therefore \quad \hat\gamma_0 = g(\hat\theta) \text{ is the MLE of } &\gamma = g(\theta) \end{aligned} $$

 

Consistency

The MLE is consistent under the regularity conditions (i.e. converge in probability to the true parameter).

In order to establish the usefulness of this property, let’s recall the definition of the Kullback-Leibler Divergence (KL divergence):

$$ D_{KL} (f ||g) = \int f(x) \text{log}\Big(\frac{f(x)}{g(x)}\Big)dx $$

From this, we can show that maximizing the likelihood function is actually equivalent to minimizing the KL divergence to the true model for large samples.

To see why this is the case,

$$ \begin{aligned} M_n(\theta) &:= \frac{1}{n} \sum_{i=1}^n \{ \text{log}f_\theta(X_i) - \text{log}f_{\theta^*}(X_i) \} \\[5pt] &= \frac{1}{n} \sum_{i=1}^n \Big\{ \text{log} \frac{f_\theta(X_i)}{f_{\theta^*}(X_i)} \Big\} \\[5pt] &\overset{p}{\to} \mathbb{E}_{f_{\theta^*}}\Big[ \text{log}\frac{f_\theta(X_i)}{f_{\theta^*}(X_i)} \Big] = -D_{KL}(f_{\theta^*} || f_\theta) \end{aligned} $$

Since KL divergence is strictly positive and has identifiability property, it is uniquely minimized when $\theta = \theta^$. Furthermore, since the MLE also asymptotically converges to the true parameter $\theta$, we can finally say that the maximum likelihood will be achieved at $\theta^*$ when the sample size is sufficiently large.

 

Asymptotic Normality (w/ Fisher Information)

The next promising property of MLE is that it is (often) asymptotically normal. To establish this fact, we need to first define what’s called the Fisher information.

First, the score function is define as the following:

$$ s_{\theta}(X) = \frac{\partial \;\text{log}_{f_\theta} (X)}{\partial \theta} $$

We can show that score function at $\theta$ has zero mean such that:

$$ \begin{aligned} 1 &= \int_\theta f_\theta(x)dx \\[10pt] \Leftrightarrow 0&= \int \frac{\partial \;\text{log}f_\theta(x)}{\partial \theta} f_\theta(x)dx \quad\quad \Big( \because (\text{log}f)^\prime = \frac{f^\prime}{f}\Big) \\[10pt] &= \mathbb{E}_\theta [s_\theta(X)] \end{aligned} $$

Then, the Fisher information is defined as just the variance of the score function.

$$ I(\theta) = Var\Big(s_\theta(X)\Big) = \mathbb{E}[s_\theta(X)^2] \quad\quad (\because \mathbb{E}[S_\theta(X)] = 0) $$

Also, under some mild regularity conditions the Fisher information can be expressed as the second order partial derivative of the log likelihood such that:

$$ \begin{aligned} &\frac{d}{d\theta} \mathbb{E}_\theta \Big[ \frac{\partial}{\partial\theta} \text{log}f_\theta(X) \Big] = 0 \\[10pt] \Leftrightarrow &\int\Big[ \frac{\partial}{\partial\theta} \Big( f_\theta(X) \frac{\partial}{\partial\theta} \text{log}f_\theta(X) \Big) \Big]dx = 0 \\[10pt] &= \int\Big[\frac{\partial}{\partial\theta}f_\theta(X) \cdot \frac{\partial}{\partial\theta} \text{log}f_\theta(X) \Big]dx + \int\Big[ f_\theta(X) \cdot \frac{\partial^2}{\partial\theta^2} \text{log}f_\theta(X) \Big]dx \\[10pt] \Leftrightarrow &\;\; \mathbb{E}_\theta\Big[ \frac{\partial^2}{\partial\theta^2} \text{log}f_\theta(X) \Big] + \mathbb{E}_\theta\Big[ \Big( \frac{\partial}{\partial\theta} \text{log}f_\theta(X) \Big)^2 \Big] = 0 \\[10pt] \therefore &\;\; I(\theta) = -\mathbb{E}_\theta\Big[ \frac{\partial^2}{\partial\theta^2} \text{log}f_\theta(X) \Big] \end{aligned} $$

So at a high level, what Fisher information does is that it measures the variance of the score function to examine how confidently we can estimate the unknown parameter. Roughly, if the log-likelihood is very flat, then even if the likelihood of our estimator is indeed very close to that of the true parameter, $\theta$ and $\hat \theta$ can still be located far apart.

On the other hand, we can see that the Fisher information depends on the unknown parameter $\theta$, so there are occasions when it cannot be computed analytically. In these cases, we define the observed fisher information as:

$$ I_n(\hat \theta) = -\frac{1}{n}\sum_{i=1}^n \Big[\frac{\partial^2}{\partial \theta^2} \text{log}f_\theta(X_i)|_{\theta=\hat \theta} \Big] $$

Then under the regularity conditions, we can show the asymptotic normality of an MLE $\hat \theta$ such that:

$$ \begin{aligned} &\sqrt{n I_n(\hat \theta)}\;(\hat \theta - \theta) \overset{d}{\to} N(0,1) \\[10pt] \Leftrightarrow \;\; &(\hat \theta - \theta) \overset{d}{\to} N\Big(0, \frac{1}{nI_n(\hat\theta)} \Big) \end{aligned} $$

Therefore, we can conclude that the (observed) Fisher information is the asymptotic variance of the maximum likelihood estimator.

The formal proof of this asymptotic normality can be found in the previous post (written in Korean).

 

Summary

We have seen various optimal properties of the MLE which makes it a great estimator when some regularity conditions are met. Namely, these are:

• MLE is invariant to a transformation
• MLE is consistent
• MLE is asymptotically normal with a variance we can compute (Fisher information)
• MLE is asymptotically unbiased and efficient (i.e. its variance attains the Rao-Cramer lower bound - discussed in previous post)

In fact, many of modern statistical theories aim to understand what will happen to the MLE when (1) the regularity conditions are not met, (2) the asymptotic theory is not valid (e.g. high-dimensional settings) and (3) when MLE is intractable to compute.

 

4.2.4. Bayes Estimators

The last general method to derive estimators is a bit different in a philosophical sense from the aforementioned two methodologies, which is the Bayes estimator. We’ll not dig into the philosophical difference between the frequentist and Bayesian as it was discussed previously in this post.

The key point is that in the Bayesian approach, we consider the parameter $\theta$ to be a random variable itself. Then, the parameter is allowed to have its own probability distribution based on our knowledge, which is often called as the prior distribution. Then it is a straightforward application of the Bayes rule to derive the posterior distribution based on the collected samples.

$$ \pi(\theta | X_1, \dots, X_n) = \frac{\pi(\theta) L(\theta | X_1, \dots, X_n) }{\int \pi(\theta) L(\theta | X_1, \dots, X_n)d\theta} $$

In practice, the integration part of the denominator of the Bayes rule cannot be solved analytically unless we restrict the prior distribution to some special families called as the conjugate family. Hence the priors are often chosen out of convenience rather than any real prior belief.

Anyhow, the derived posterior distribution is a distribution over the possible parameter values upon seeing the collected samples. Then with respect to point estimation, a Bayes estimator is just some kind of a summary statistic of the posterior distribution where one common candidate is the posterior mean.

 

<Example>

Let’s take a quick look at example of a Binomial Bayes estimator.

Suppose we have $X_1, \dots, X_n \sim Bernoulli(p)$. Then the binomial likelihood (distribution of the samples) is written as:

$$ \begin{aligned} f(X_1, \dots, X_n | p) &= \prod_{i=1}^n p^{X_i} (1-p)^{1-X_i} \\[5pt] &= p^{n\bar X} (1-p)^{n(1-\bar X)} \end{aligned} $$

Now we have to specify a prior distribution for the parameter $p$.

The first choice is the uninformative prior such that $\pi(p) \propto 1$ for $0 \leq p \leq 1$. The posterior distribution for this case is:

$$ \begin{aligned} f(p | X_1, \dots, X_n) &\propto p^{n\bar X} (1-p)^{n(1-\bar X)} \\[5pt] &= p^{(n\bar X + 1) - 1} (1-p)^{(n(1-\bar X) + 1) -1} \\[10pt] &\sim \text{Beta}(n\bar X + 1, n(1-\bar X)+1) \\[10pt] \Rightarrow \hat p = \frac{n\bar X + 1}{n+2} &= \frac{n}{n+2}\bar X + \frac{2}{n+2} \cdot\frac{1}{2} \end{aligned} $$

Thus we have our Bayes estimator (posterior mean) from the property of beta distribution, which is a weighted average of the MLE of the parameter $p$, and mean of the prior (uniform).

Another natural choice for the $p$ is the Beta distribution which conjugate to the Binomial likelihood. By specifying a beta prior $\pi(p) \sim \text{Beta}(\alpha, \beta)$, the posterior distribution is (proof):

$$ \begin{aligned} f(p | X_1, \dots, X_n) &\sim \text{Beta}(\alpha + n\bar X,\; \beta+n(1-\bar X)) \\[10pt] \Rightarrow \hat p &= \frac{\alpha + n\bar X}{\alpha + \beta + n} \\[5pt] &= \Big(\frac{\alpha + \beta}{\alpha + \beta + n} \cdot \frac{\alpha}{\alpha + \beta}\Big) + \Big(\frac{n}{\alpha + \beta + n}\bar X\Big) \end{aligned} $$

We can similarly decompose the estimator to show that the Bayes estimator is a compromise between the prior and the likelihood.

 

---

4.3 Evaluating Estimators

 

4.3.1. Loss function and risk

Okay so by now, we know that there can be multiple ways to define an estimator which are all statistically valid. Then how can we evaluate these different estimators?

One key idea from the decision theory is to minimize the expected loss for an action $a$ under the parameter $\theta$. So basically, the loss function is measuring how far is the taken action from the true target. By focusing on the point estimation, the loss function will roughly return a large value if $a$ is far from $\theta$ and small if our guess (action) is good.

To this end, there can be various choices of the loss function where some of the most common ones are:

$$ \begin{aligned} \text{1. Squared Loss}: L(a, \theta) &= (a-\theta)^2 \\[10pt] \text{2. Absolute Loss}: L(a, \theta) &= |a-\theta| \end{aligned} $$

We can define some custom loss functions such that if we want to penalize errors more for small values of $\theta$, then the loss function can be something like:

$$ L(a, \theta) = \frac{(a - \theta)^2}{|\theta| + 1} $$

Anyways, once we have a loss function and an estimator $\hat \theta (X)$, we define the risk as the expected value of the loss function as:

$$ R(\theta, \hat \theta(X)) = \mathbb{E}_\theta\Big[ L(\hat\theta(X), \theta) \Big] $$

Naturally, we would want to find an estimator $\hat\theta$ that has the smallest risk compared to any other estimators $\tilde\theta$ such that:

$$ R(\theta, \hat\theta(X)) \leq R(\theta, \tilde\theta(X)) $$

, albeit such an optimal estimator rarely exists for real problems.

 

<Example>

To better understand what we’ve been doing so far, let’s consider the problem of Bernoulli estimation where we want to compare the performance of MLE and Bayes Estimator (w/ Beta prior).

As we have derived earlier, the estimators are:

$$ \begin{aligned} \text{MLE}&: \hat p_1 = \frac{1}{n}\sum_{i=1}^n X_i \\[10pt] \text{Bayes Estimator}&: \hat p_2 = \frac{n\bar X + \alpha}{n + \alpha + \beta} \end{aligned} $$

Let’s consider a squared loss of the two estimators:

$$ \begin{aligned} R(p, \hat p_1) &= \frac{p(1-p)}{n} \\[10pt] R(p, \hat p_2) &= \text{Var}\Big( \frac{n\bar X + \alpha}{n + \alpha + \beta} \Big) + \Big( \mathbb{E}\Big[ \frac{n \bar X + \alpha}{n + \alpha + \beta} \Big] - p \Big)^2 \\[10pt] &=\frac{n}{4(n + \sqrt{n})^2}, \quad (\text{let }\alpha=\beta=\sqrt{\frac{n}{4}}) \end{aligned} $$

Okay, so the results shows that we cannot clearly distinguish the winner as neither estimators dominate the other. For instance, the MLE $\hat p_1$ is better if $p$ is close to 0 or 1, whereas the Bayes estimator $\hat p_2$ is better when $p \approx 0.5$.

Hence, we need some extra criteria to find the single “best” estimator.

 

4.3.2. Admissibility

At a high-level, we can think of a guardrail criteria to weed out the really useless estimators in the first place. Specifically, it seems natural to disregard an estimator $\hat \theta_1$ if there exists another estimator $\hat \theta_2$ such that

$$ \begin{aligned} R(\theta, \hat \theta_2) &\leq R(\theta, \hat\theta_1), \quad \text{ for every }\theta \in \Theta \\[5pt] R(\theta, \hat \theta_2) &< R(\theta, \hat\theta_1), \quad \text{ for some }\theta \in \Theta \end{aligned} $$

, which is equivalent to saying that the performance of $\hat theta_2$ is at least not worse than $\hat \theta_1$. In this sense, estimators like $\hat \theta_1$ are called inadmissible, whereas $\hat\theta_2$ is admissible.

However, admissible estimators are not unique so we need to further narrow our search for the optimal ones beyond admissibility.

 

4.3.3. Minimax Risk

The minimax estimator $\hat \theta(X)$ is one that minimizes the worst-case risk such that

$$ \underset{\theta \in \Theta}{\text{sup}} R(\theta, \hat\theta(X)) = \underset{\tilde \theta}{\text{inf}} \; \underset{\theta \in \Theta}{\text{sup}} \; \mathbb{E}_\theta\Big[ L(\theta, \tilde\theta(X)) \Big] $$

What this implies is that the minimax estimator is the smallest of all the estimators that minimizes the expected loss for the worst performing parameter $\theta$.

This is one of the dominant paradigms for evaluating estimators because we can actually find the minimax estimator (at least up to constants) for many problems of interest. This will be discussed in detail after we take a look at the Bayes risk.

 

4.3.4. Bayes Risk

The Bayes risk of an estimator is defined as its risk averaged over a prior $\pi(\theta)$:

$$ R_\pi(\hat \theta) = \mathbb{E}_{\theta\sim\pi}\Big[R(\theta, \hat\theta(X)) \Big] $$

In this sense, the Bayes estimator is the one that minimizes this Bayes risk.

For example, suppose $\theta \sim \pi$ and $X \sim f_\theta$.

$$ \text{Let } m(X) = \int\pi(\theta)f_\theta(X)d\theta, \quad (\text{marginal likelihood}) $$ $$ \begin{aligned} \Rightarrow R_\pi(\hat\theta) &= \int_\theta R(\theta, \hat \theta(X))\pi(\theta)d\theta \\[5pt] &= \int_\theta \Big[ \int_X L(\theta, \hat\theta(X)) f_\theta(X)dX \Big] \pi(\theta)d\theta \\[5pt] &= \int_X\Big[ \int_\theta L(\theta, \hat \theta) \pi(\theta | X)d\theta \Big] m(X)dX, \quad (\because f_\theta(X)\pi(\theta) = \pi(\theta|X)m(X)) \end{aligned} $$

Then we can ignore the integration w.r.t. $X$ since it is independent of the parameter $\theta$. Thus, the Bayes estimator by definition, minimizes the integration such that:

$$ \hat\theta(X) = \underset{\tilde \theta}{\text{argmin}} \int_{\theta} L(\theta, \tilde \theta(X)) \pi(\theta | X)d\theta $$

, where the term on the right hand side is called as posterior expected loss (loss $\times$ posterior).

A simple but important special case is that with respect to the squared loss function, the Bayes estimator is the conditional expectation (i.e. posterior mean) as we have seen earlier.

$$ \hat \theta(X) = \mathbb{E}[\theta|X] $$

 

<Example>

To see how the Bayes risk can be applied, let’s revisit the Bernoulli estimator from the earlier example. We have derived:

$$ \begin{aligned} \text{MLE}&: \hat p_1 = \frac{1}{n}\sum_{i=1}^n X_i \\[10pt] \text{Bayes Estimator}&: \hat p_2 = \frac{n\bar X + \alpha}{n + \alpha + \beta} \end{aligned} $$

where the corresponding risk was:

$$ \begin{aligned} R(p, \hat p_1) &= \frac{p(1-p)}{n} \\[10pt] R(p, \hat p_2) &=\frac{n}{4(n + \sqrt{n})^2}, \quad (\text{let }\alpha=\beta=\sqrt{\frac{n}{4}}) \end{aligned} $$

In this setting, suppose we take the uniform prior for the parameter $\theta$. Then:

$$ \begin{aligned} \pi(p) &\sim \text{Uniform}(0,1) \\[20pt] R_\pi(\hat p_1) &= \int_{0}^1 \frac{p(1-p)}{n}dp = \frac{1}{6n} \\[10pt] R_\pi(\hat p_2) &= \frac{n}{4(n+\sqrt{n})^2} \end{aligned} $$

Thus, we can conclude that for large sample sizes, the MLE $\hat p_1$ has smaller Bayes risk. However, for the worst-case risk (i.e. $p=1/2$), $R(\hat \theta_2)$ is always less than 1/4, so it is better than $\hat \theta_1$. So again, we don’t have a clear winner.

Comparison of MLE vs Bayes Estimator

 

---

4.4 Strategies to find Minimax Estimators

 

4.4.1. Bounding the Minimax Risk

One strategy to find the minimax estimator is by finding upper and lower bounds on the minimax risk and show that those are indeed equivalent. Then, we can say that the estimator that achieves the upper bound is indeed a minimax estimator.

As an example, let’s consider a classical result that if we observed independent draws from a d-dimensional Gaussian $X_1, \dots, X_n \sim N(\theta, I_d)$, then the sample mean is a minimax estimator of $\theta$ with respect to the squared loss.

To prove why this is the case, the overall procedure is as follows:

$$ \begin{aligned} &1. \text{ (Upper Bound) Compute the risk of }\hat \theta \\ &\quad\quad \Rightarrow \underset{\tilde\theta}{\text{inf}} \; \underset{\theta}{\text{sup}} \; R(\theta, \tilde\theta) \leq R(\theta, \hat\theta) \\[10pt] &2. \text{ (Lower Bound) Compute the Bayes risk of the Bayes estimator for some prior } \\ &\quad\quad \Rightarrow \mathbb{E}_{\pi(\theta)}\Big[ R(\theta, \tilde \theta_{Bayes}) \Big] \leq \underset{\tilde\theta}{\text{inf}} \; \underset{\theta}{\text{sup}} \; R(\theta, \hat\theta) \\[10pt] &3. \text{ Show upper bound = lower bound} \end{aligned} $$

After some tedious calculation, we get the following inequality for a risk $R_n$:

$$ \frac{d}{n(1 + \frac{1}{nc^2})} \leq R_n \leq \frac{d}{n} $$

Since $c$ is an arbitrary constant, by taking $c \to \infty$ the minimax risk is upper and lower bounded by the same quantity $d/n$ and hence the sample average $\hat \theta$ is minimax.

 

4.4.2. Least Favorable Prior

Another way to obtain the minimax estimators is by constructing what are called “least favorable priors”. The definition is :

$$ \begin{aligned} &\textbf{(Theorem)} \\[10pt] &\text{Let }\hat \theta \text{ be the Bayes estimator for some prior } \pi. \\[5pt] &\text{If }R(\theta, \hat\theta) \leq B_\pi(\hat \theta) \text{ for all }\theta, \text{ then }\hat\theta \text{ is minimax and }\pi \text{ is called a } \textbf{least favorable prior.} \end{aligned} $$

 

This can be proved by the contradiction that if $\hat \theta$ is not minimax, then there exists another estimator $\hat \theta_0$ such that:

$$ \underset{\theta}{\text{sup}} \;R(\theta, \hat\theta_0) < \underset{\theta}{\text{sup}} \;R(\theta, \hat\theta) $$

Since the average of a function (posterior mean) is always less than or equal to its maximum, we have

$$ B_\pi(\hat\theta_0) \leq \underset{\theta}{\text{sup}} \;R(\theta, \hat\theta_0) $$

Thus,

$$ \begin{aligned} &B_\pi (\hat \theta_0) \leq \underset{\theta}{\text{sup}} \;R(\theta, \hat\theta_0) < \underset{\theta}{\text{sup}} \; R(\theta, \hat\theta) \leq B_\pi(\hat \theta) \\[10pt] \Rightarrow &B_\pi (\hat \theta_0)\leq B_\pi(\hat \theta) \end{aligned} $$

which is a contradiction.

A resulting consequence is that if the risk is constant, then the Bayes estimator $\hat \theta$ is minimax.

 

---

4.5 Nonparametric Estimation

In this section, we are going to discuss nonparametric estimation of the following estimands:

• cumulative distribution functions (CDF)
• regression functions

 

4.5.1. Estimation of Cumulative Distribution Functions (CDF)

Let’s start with the estimation of cumulative distribution functions. Formally, given $X_1, \dots, X_n \overset{i.i.d.}{\sim} F$, we would like to estimate the cumulative distribution function $F(x) = P(X \leq x)$.

Note that since we are working within the “non-parametric” framework, we are not going to impose any restrictions of $F$, neither we have any parameters to estimate.

Then, it becomes that our estimator for the CDF is just the empirical CDF. The statistical implication of “emphirical” corresponds to the probability mass function that puts equal mass of $1/n$ over each of the data points $X_i$:

$$ \hat F_n(x) = \frac{\sum_{i=1}^n \mathbb{1}(x_i \leq x) }{n} $$

This can be regarded as a sample mean of the independent Bernoulli random variables with probability $p = P(X \leq x)$.

Okay, so let’s investigate some basic properties of this emphirical estimator. For fixed values of $x$ we have:

$$ \begin{aligned} &1.\textbf{ Bias:} \text{ The estimator we have proposed is unbiased:} \\[5pt] &\quad\quad\quad\quad \Rightarrow \mathbb{E}\Big[\hat F_n(x) \Big] = \frac{\sum_{i=1}^n \mathbb{E}[\mathbb{1}(X_i \leq x) ] }{n} = P(X \leq x) \\[30pt] &2.\textbf{ Variance:} \text{ The variance of the estimator is:} \\[5pt] &\quad\quad\quad\quad \Rightarrow \text{Var}\Big[\hat F_n(x) \Big] = \frac{ P(X \leq x)(1-P(X \leq x)) }{n} ,\quad\quad (\because \text{Variance of Binomial distribution}) \\[30pt] &3.\textbf{ MSE:} \text{ The MSE at } x \text{ is same as the variance (unbiased)}: \\[5pt] &\quad\quad\quad\quad \Rightarrow \text{MSE} = \frac{ P(X \leq x)(1-P(X \leq x)) }{n} \to 0, \quad \text{as } n\to \infty \\[30pt] \end{aligned} $$

Using this result and the Chebyshev’s inequality, we can conclude that our emphirical estimator converges in probability to the true CDF:

$$ P\Big( |\hat F_n(x) - F(x)| \geq \epsilon \Big) \to 0, \quad \text{as }n\to\infty $$

A slight extension of this result is the Glivenko-Cantelli theorem, which states that the empirical CDF converges to the true CDF uniformly (i.e. not just for a fixed values of $x$, but for every $x$ simultaneously):

$$ \underset{x \in \mathbb{R}}{\text{sup}} |F(x) - \hat F_n (x)| \to 0 \quad \text{almost surely}. $$

(Note that almost-sure convergence implies convergence in probability)

Also, it has been proven that the asymptotic distribution of the emphirical CDF can be attained in a closed form for the case when the underlying distribution is continuous. Namely, it holds that:

$$ \underset{n \to \infty}{\text{lim}} P\Big( \sqrt{n}\; \underset{x \in \mathbb{R}}{\text{sup}} \; |F(x) - \hat F_n(x)| \geq \epsilon \Big) = 2\sum_{j=1}^\infty (-1)^{j-1} \text{exp}(-2j^2 \epsilon^2). $$

This is a “distribution-free” result, meaning that it remains the same no matter what the shape of the distribution is, as long as it’s continuous.

 

4.5.2. Estimation of Statistical Functionals (Plug-in estimators)

Next, we are going to take a look at how we can use the empirical CDF to estimate statistical functionals.

We can think of the “functional” as a mapping from a function to a real number. So it takes function as an input and returns a real number such that:

$$ T(f): f \mapsto \mathbb{R} $$

Thus, a statistical functional typically refers to a function of the CDFs.

Some classical examples are:

$$ \begin{aligned} &1. \textbf{ Mean:} \quad \mu(F) = \int x\;dF(x) \quad\Big( = \int xf(x)dx \Big) \\[10pt] &2. \textbf{ Variance:} \quad \text{Var}(F) = \int (x-\mu(F))^2 \; dF(x) \\[20pt] \end{aligned} $$

Okay, then how can we estimate these kinds of functionals? A natural estimator is to consider the “plug-in principle” .

The plug-in principle is a technique widely used in statistics to estimate a feature of a probability distribution that cannot be computed exactly. So roughly, the core idea of plug-in principle is that a feature of a given distribution can be approximated by the same feature of the empirical distribution of a sample of observations drawn from the given distribution (reference).

Then, the feature of the empirical distribution is called as a plug-in estimator. For instance, a skewness or a correlation of a given distribution can be approximated by the analogous statistic of the empirical distribution such that:

$$ \begin{aligned} &1. \textbf{ Skewness:} \\[5pt] &\quad \Rightarrow \quad \kappa = \frac{\mathbb{E}(X-\mu)^3}{\sigma^3} = \frac{\mathbb{E} (X-\mu)^3}{(\mathbb{E}(X-\mu)^2)^{3/2}} \\[5pt] &\quad \Rightarrow \quad \hat \kappa = \frac{\frac{1}{n} \sum_{i=1}^n (X_i - \hat\mu)^3 }{(\frac{1}{n} \sum_{i=1}^n(X_i - \hat \mu)^2)^{3/2} } \\[30pt] &2. \textbf{ Correlation:} \\[5pt] &\quad \Rightarrow \quad \rho = \frac{\mathbb{E}(X-\mu_X)(Y - \mu_Y)}{\sigma_X\sigma_Y} \\[5pt] &\quad \Rightarrow \quad \hat \rho = \frac{\sum_{i=1}^n (X_i - \hat \mu_X)(Y_i-\hat \mu_Y) }{\sqrt{\sum_{i=1}^n (X_i - \hat \mu_X)^2} \sqrt{\sum_{i=1}^n(Y_i-\hat \mu_Y)^2}} \end{aligned} $$

Note that these estimators are completely free of any parametric assumptions.

 

4.5.3. Estimation of regression functions

The next topic we are going to look at is the non-parametric estimation of regression functions.

Typically, a regression study is to find the relationship between the response $Y$ and covariate $X$ via the regression function $R(x)$ such that:

$$ R(x) = \mathbb{E}[Y | X=x] = \int yf(y|x)dy. $$

In this sense, the goal of regression analysis is to “estimate” the regression function based on observations.

One of the most basic ways to estimate this function non-parametrically is the kernel regression. For simplicity, let’s suppose we only have one covariate, then the estimator is defined as

$$ \hat R(x) = \sum_{i=1}^n w_i(x)Y_i $$

, which is called “linear smoother” in the literatures.

Then, the reason why it’s called as “kernel” regression is because the weights are chosen according to a prespecified kernel such as the Gaussian kernel or spherical kernel et cetera. More specifically, the weights are defined as:

$$ w_i(x) = \frac{K(\frac{x-X_i}{h})}{\sum_{j=1}^n K(\frac{x-X_i}{h}) } $$

, where bandwidth $h$ controls the amount of smoothing (i.e. larger $h$, smoother function).

 

<Example>

Let’s quickly look at an example of a simple kernel regression to examine its performance over the parametric counterparts.

Suppose we have the following design:

$$ y_i = R(x_i) + \epsilon_i $$

Furthermore, we add some additional assumptions for computational convenience:

• $x_i$ is one-dimensional and equally spaced on [0, 1]

• The function $R(x)$ is L-Lipschitz, that there exists some constant $L$ such that:

  $$ \Big| \frac{d}{dx}R(x) \Big| \leq L $$

• The noise is i.i.d with zero mean and constant variance $\sigma^2$

• The regression kernel used is the spherical kernel :

$$ K(x) = \mathbb{1}(-1 \leq x \leq 1) $$

With above setting and $h \geq 1/n$, the MISE (Mean Integrated Squared Error) of our estimator for regression function is upper bounded by (w/o proof):

$$ \begin{aligned} Risk(\hat R, R) &= \int_{0}^1 \{\hat R(x) - R(x) \}^2dx \\[5pt] &= \int_0^1 \text{bias}^2(x) \;dx + \int_0^1 \text{Var}\Big(\hat R(x)\Big)dx \leq L^2h^2 + \frac{\sigma^2}{nh} \end{aligned} $$

To obtain an exact bound, we further need to designate the bandwidth $h$ (suppose $L$ and $\sigma^2$ is fixed). A natural choice is to choose the value of $h$ that minimizes this risk, which is:

$$ \begin{aligned} h = \Big( \frac{\sigma^2}{2nL^2} \Big)^{1/3}, \end{aligned} $$

then by plugging in this value, we have:

$$ \begin{aligned} Risk(\hat R, R) \leq 2\Big(\frac{L\sigma^2}{n} \Big)^{2/3} \end{aligned} $$

Interestingly, this result reveals something fundamental about non-parametric methodologies. We can see that with an optimally chosen bandwidth, the MISE decreases to zero at a rate of $n^{-2/3}$.

On the other hand, most of the parametric estimators have the convergence rate of $n^{-1}$. So by putting the results together, we can conclude that the slower rate of convergence can be regarded as a pay-off of being free of parameters. Furthermore, the procedure of finding the optimal tuning parameters is often very challenging to be analyzed theoretically.

 

4.6 Consistency in Nonparametric Bootstrap

The last topic we are going to cover in this pose is the bootstrap method, which is a powerful tool for computing standard errors and confidence intervals.

There are many types of bootstrapping procedures developed for various purposes, but here we are going to focus on the most popular bootstrap method originally suggested by Efron (1979).

 

<Definition>

$$ \begin{aligned} &\text{Let }X_1, \dots, X_n \overset{i.i.d.}{\sim}F \;\text{ and }\; T(X_1, \dots, X_n;F) \text{ be a given functional.} \\[10pt] &\text{Then, the bootstrap distribution of }T \text{ is defined as} \\[10pt] &\Rightarrow H_{Boot}(x) = P\Big\{ T(X_1^*, \dots, X_n^*;F_n) \leq x \; | \; X_1, \dots, X_n \Big\} := P_{F_n}\Big\{ T(X_1^*, \dots, X_n^*;F_n) \leq x \Big\} \\[5pt] &\quad\;, \text{where } X_1^*, \dots, X_n^* \text{ is an i.i.d. sample of size }n \text{ from the empirical distribution }F_n \text{ based on }X_1, \dots, X_n. \end{aligned} $$

 

By its definition, the bootstrap distribution is a conditional distribution given the observations $X_1, \dots, X_n$, which makes the bootstrap distribution itself as a random quantity dependent on the samples.

Intuitively, it is helpful to think of the bootstrap distribution as a histogram of functionals $T_1, \dots, T_B$, where each $T_i$ is computed using the bootstrap samples drawn from the original samples with replacement.

An exact computation of bootstrap distribution is practically infeasible for a large sample size $n$, so people often use an approximation using Monte-Carlo repetitions for sufficient bootstrap sample size $B$ (e.g. $B=1000$).

The reason why this kind of approximation is possible can theoratically be proved using the Glivenko-Cantelli theorem we have seen earlier. Although the detailed proof will not be discussed here, the well known result is that:

$$ \underset{x \in \mathbb{R}}{\text{sup}} \Big| \hat H_{Boot}(x) - H_{Boot}(x) \Big| \; \overset{a.s.}{\to} \; 0,\; \text{ as }\; B\to\infty $$

 

4.6.1. The Kolmogorov metric and consistency

Okay, so let’s dive in a little deeper into the consistency of the bootstrap distribution as a function estimator.

Suppose that we have $F$ and $G$ which are two CDFs on a specific sample space. For $X_1, \dots, X_n \overset{i.i.d.}{\sim} F$ and a given functional $T(X_1, \dots, X_n;F)$, let

$$ \begin{aligned} H_n(x) &= P\Big\{ T(X_1, \dots, X_n \;;F) \leq x \Big\}, \\[10pt] H_{Boot}(x) &= P\Big\{ T(X_1^*, \dots, X_n^* \;;F_n) \leq x \;| X_1, \dots, X_n \Big\} \end{aligned} $$

Then for some metric $\rho(F, G)$, we say that the bootstrap estimator is consistent under $\rho$ if

$$ \rho(H_n, H_{Boot}) \;\overset{p}{\to}\;0, \;\text{as }n\to\infty $$

To this end, the Kolmogorov metric is one commonly used metric in the literatures along with the Wasserstein metric, which is defined as:

$$ \text{Kolm}(F, G) = \underset{-\infty < x< \infty}{\text{sup}} \Big | F(x) - G(x) \Big| $$

This metric is somewhat a stronger notion of distance in order to characterize the convergence.

Suppose that $X_n \sim F_n$ and $X \sim F$. For any given $x_0 \in \mathbb{R}$, we have

$$ |F_n(x_0) - F(x_0)| \leq \text{Kolm}(F_n, F) $$

, which implies that convergence in the Kolmogorov metric implies $X_n \overset{d}{\to} X$.

 

4.6.2. Example: the sample mean

Using this Kolmogorov metric, we can show that the bootstrap estimator for a sample mean is consistent such that:

$$ \begin{aligned} &\text{Suppose that }X_1, \dots, X_n \overset{i.i.d.}{\sim} F \;\text{ and that }\mathbb{E}_F[X^2] <\infty, \\[10pt] &\text{and let } T(X_1, \dots, X_n\;;F) = \sqrt{n}(\bar X - \mu). \\[10pt] &\text{Then, we have }\; \text{Kolm}(H_n, H_{Boot}) \overset{a.s.}{\to} 0 \text{ as }n\to\infty \end{aligned} $$

The proof of this theorem was originally introduced in Singh (1981) and Bickel and Freedman (1981), and here I’ll briefly mention the overall idea of the proof.

Let’s denote $T_n = \sqrt{n}(\bar X - \mu)$ and $T_n^* = \sqrt{n}(\bar X^* - \bar X)$. Moreover, we denote $\sigma^2$ and $s^2$ be the variances of $F$ and $F_n$ respectively.

Then we can apply the triangle inequality to the Kolmogorov metric such that:

$$ \begin{aligned} \text{Kolm}(H_n, H_{Boot}) &= \underset{-\infty < x< \infty}{\text{sup}} \Big| P_F(T_n \leq x) - P_{F_n}(T_n^* \leq x) \Big| \\[10pt] &\leq \underset{-\infty < x< \infty}{\text{sup}} \Big| P_F\Big(\frac{T_n}{\sigma} \leq \frac{x}{\sigma}\Big) \Big| + \underset{-\infty < x< \infty}{\text{sup}} \Big| \Phi\Big(\frac{x}{\sigma}\Big) \leq \Phi\Big(\frac{x}{s}\Big) \Big| \\[5pt] &\quad + \underset{-\infty < x< \infty}{\text{sup}} \Big| \Phi\Big(\frac{x}{s}\Big) - P_{F_n}\Big(\frac{T_n^*}{s} \leq \frac{x}{s}\Big) \Big| \\[10pt] &\equiv A_n + B_n + C_n \end{aligned} $$

Then in order to claim:

$$ \text{Kolm}(H_n, H_{Boot}) \overset{a.s.}{\to} 0 \;\text{ as } n\to\infty $$

, it is sufficient to instead show that:

$$ A_n, B_n, C_n \overset{a.s.}{\to} 0 \;\text{ as } n\to\infty $$

which indeed is the case, as proven in the paper of Bickel and Freedman (1981).

 

4.6.3. Failure of bootstrap

Although the ordinary bootstrap is constant for many of the important functionals, there are some rare cases when this condition is not satisfied, i.e. bootstrap estimator is not consistent.

As an example, let $X_1, \dots, X_n \overset{i.i.d.}{\sim} Unif(0, \theta)$ and $T_n = n(\theta - X_{(n)})$, where $X_{(n)}$ is the maximum of $X_1, \dots, X_n$.

Then it is straightforward to see that:

$$ \begin{aligned} P(T_n \leq t) &= P\Big(\theta - X_{(n)} \leq \frac{t}{n}\Big) \\[5pt] &= P\Big(X_{(n)} \geq \theta - \frac{t}{n}\Big) \\[5pt] &= 1 - P\Big(X_{(n)} < \theta - \frac{t}{n}\Big) \\[5pt] &= 1 - \Big\{P\Big(X_{(1)} < \theta - \frac{t}{n}\Big) \Big \}^n \\[5pt] &= 1 - \Big(1-\frac{t}{n\theta}\Big)^n \end{aligned} $$

Therefore, the theoretical limiting distribution of the statistic is:

$$ \underset{n\to\infty}{\text{lim}} P_F(T_n \leq t) = 1 - e^{-t/\theta} $$

which is a cumulative distribution function of the exponential distribution $\text{Exp}(\frac{1}{\theta})$.

On the other hand, let’s derive the limiting distribution of the bootstrap estimator $T_n^* = X_{(n)} - X_{(n)}^*$ when $\theta = 1$:

$$ \begin{aligned} P_{F_n}\Big(T_n^* \leq t \;|X_1,\dots,X_n \Big) &\geq P_{F_n}\Big( T_n^* = 0 \;|X_1,\dots,X_n\Big) \\[10pt] &= P_{F_n}\Big( X_{(n)}^* = X_{(n)} \;|X_1,\dots,X_n \Big) \\[10pt] &= 1 - P_{F_n}\Big( X_{(n)}^* \neq X_{(n)} \;|X_1,\dots,X_n \Big) \\[10pt] &= 1 - P_{F_n}\Big( X_{(n)}^* < X_{(n)} \;|X_1,\dots,X_n \Big), \quad (\because X_{(i)}^* < X_{(i)}) \\[10pt] &= 1 - \Big(1-\frac{1}{n} \Big)^n \\[10pt] &\to 1 - e^{-1} \end{aligned} $$

Now, let’s suppose we take $t = 0.0001$. Then the limiting distribution of the bootstrap estimator is at least greater than $1 - e^{-1}$, whereas the theoretical limiting distribution is $1 - e^{-0.0001} \approx 0$.

From this result, we can conclude that the asymptotic bootstrap statistic $T_n^*$ is in fact different from the theoretical limiting distribution $T_n$. This clearly shows the failure of bootstrap method for this specific problem.

 

 

---

Reference

• Casella, G., & Berger, R. L. (2002). Statistical inference. 2nd ed. Australia ; Pacific Grove, CA: Thomson Learning.