[A/B Test] 다중 검정의 통계적 보정

    2022, Apr 29

    저번 포스트에서 실험의 결과를 도출하는 과정에서 발생할 수 있는 다중 검정의 개념과, 이를 처리할 수 있는 몇가지 통계적 접근법들에 대해서 살펴보았다. 해당 내용의 연장선상에서, 이번에는 구체적으로 어떠한 경우에 다중 검정에 대한 유의 수준 보정이 필요한지를 정리해보도록 하겠다.

    앞서 다중 검정은 그 개념 자체가 다소 생소하기 때문에 A/B Test와 관련한 실무자들에게 그 위험성 자체가 인지되지 않는 경우가 많다는 점을 언급한 적이 있다. 그리고 실제로 optimizely, facebook ads 등의 실험 플랫폼 등에서도 구체적인 p-value를 제시하기 보다는 최종적인 결과 (통계적으로 유의하다 / 유의하지 않다) 만을 UI 상에서 제시하기 때문에, 구체적으로 어떠한 부분에서 다중 검정으로 인한 유의 수준이 보정되는지를 파악하기가 다소 어렵다.

    이러한 측면에서 A/B Test를 설계 및 진행함에 있어 어떠한 측면에서 어떻게 다중 검정의 이슈를 핸들링할 수 있는지를 개괄적으로 정리해보려고 한다. 구체적으로 다룰 내용은 다음과 같다:

     

    1. Metric Type

    이전에 살펴본 Bonferroni 등의 방법을 사용해서 다중검정 문제를 해결하려는 경우, 필연적으로 우리는 더 낮은 유의수준에서 가설 검정을 진행하게 된다. 이에 따라 결과적으로 실험의 유의성을 주장하기 위해서는 더 유의한 (낮은) p-value가 요구되기 때문에 실험의 검정력을 손해보는 상황이 발생한다. 이와 같은 이유로 Bonferroni 등의 방법은 정말 필요할 때만, 최소한으로 적용하는 것이 바람직할 것이다. 무분별하게 적용할 경우면 실제로 유의했던 실험들이 기각되는 오류가 발생할 수 있기 때문이다.

    이러한 맥락에서 각 지표들을 그 특징에 따라 분류한 다음, 특정한 지표가 실험의 결론에 핵심적인 영향을 미치는지, 또는 단순히 참고용으로만 활용되는지에 따라서 다중 검정에 대한 유의수준 보정이 필요할 수도, 필요하지 않을 수도 있다. 이에 대해 하나씩 살펴보자.

     

    1차 유효성 평가변수 (Primary Metric)

    OEC(Overall Evaluation Criterion)와 같이 실험을 통해 인과성을 검증하고자 하는 메인 지표를 의미한다.

    이러한 지표들에 대해서 만큼은 1종 오류가 실험의 계획단계에서 고려된 유의수준보다 절대로 증가해서는 안될 것이다.

    보통의 A/B Test에서 1차 유효성 평가변수는 단 한개만 설정되는 것이 일반적이나, 만약 후술할 2차 유효성 평가변수 등에 대한 확증적 결과를 얻으려는 경우 앞서 살펴본 방법론들을 바탕으로 함께 유의수준을 보정해야 할 필요가 있다.

     

    2차 유효성 평가변수 (Secondary Metric)

    2차 유효성 평가변수란, 1차 유효성 평가변수에 비해서는 중요도가 떨어지지만 그럼에도 불구하고 관심있게 체크하고 싶은 지표를 의미한다.

    일반적으로 이러한 2차 유효성 평가변수에 대해서는 유의수준을 보정하지 않는 것이 원칙이나, 그럼에도 불구하고 실험의 유의성을 판단함에 있어 직접적인 고려대상이 되는 경우에는 다중 검정을 보정해야 한다.

     

    보조 지표 (Debugging & Guardrail Metric)

    Guardrail metric 등의 보조 지표에 대해서는 유의수준을 보정할 필요가 없다.

    해당 지표들은 실험의 유의성을 판단하는데 있어 직접적인 영향을 미치지 않는, 어디까지나 “부수적인” 지표이기 때문에 1종 오류의 증가에 민감하게 대응할 필요가 없다. 그렇기 때문에 이러한 지표들에 대한 결과는 어디까지나 참고용으로만 활용해야 한다.

     

    2. Segment Analysis

    많은 경우, 진행된 실험의 모집단에서 하위군 (subgroup) 별로 결과를 파악하고 싶은 경우가 발생할 수 있다. 구글 애널리틱스, Optimizely, 어도비 등 여러 실험 플랫폼들 대부분 하위군 분석을 지원하기는 하지만, 구체적인 결과가 어떤식으로 산출되는지에 대한 레퍼런스는 생각보다 많이 없었다. 따라서 해당 섹션에서는 일반적인 맥락에서 하위군 분석(Segment Analysis)을 수행함에 있어 유의해야 할 점 몇 가지를 정리해보도록 하겠다.

     

    2.1. Segment Analysis의 분류

    하위군 분석은 그 목적에 따라 크게 다음의 두가지로 구분될 수 있다. 통계적 오류에 빠지지 않기 위해서는 이를 확실하게 구별하는 것이 중요하다.

     

    (a) Exploratory Segment Analysis (탐색적 하위군 분석)

    탐색적 하위군 분석이란, 다중 검정을 실시하지만 다중성을 보정하지 않는 하위군 분석을 의미한다. 사실 A/B Test에서 약 90%는 탐색적 하위군 분석이라고 봐도 무방할 것이다.

    탐색적 하위군 분석의 가장 큰 목적은 다음의 질문에 대해 대답을 하기 위함이다.

    Q. treatment effect가 각 하위군 별로 일정한가?

    사실 이를 알아보기 위한 가장 정확한 통계 방법은 ANOVA 모형을 바탕으로 interaction effect의 회귀 계수의 기울기가 $0$인지 아닌지 여부를 검정하는 것이지만, 많은 경우 플랫폼 사용자들이 통계 비전공자라는 점에서 이는 결과 해석의 혼란을 초래할 수 있다.

    따라서 현실적인 대안으로, optimizely 등의 플랫폼에서는 UI 상에서 각 하위군들의 검정 결과에 대한 p-value를 명시적으로 제시하는 것은 지양하고, 신뢰구간으로 통계적 유의성만을 보여주는 방식을 채택하고 있다. 이는 플랫폼의 사용자가 하위군 분석 결과를 확증적으로 받아들이지 않도록 하기 위함이다.


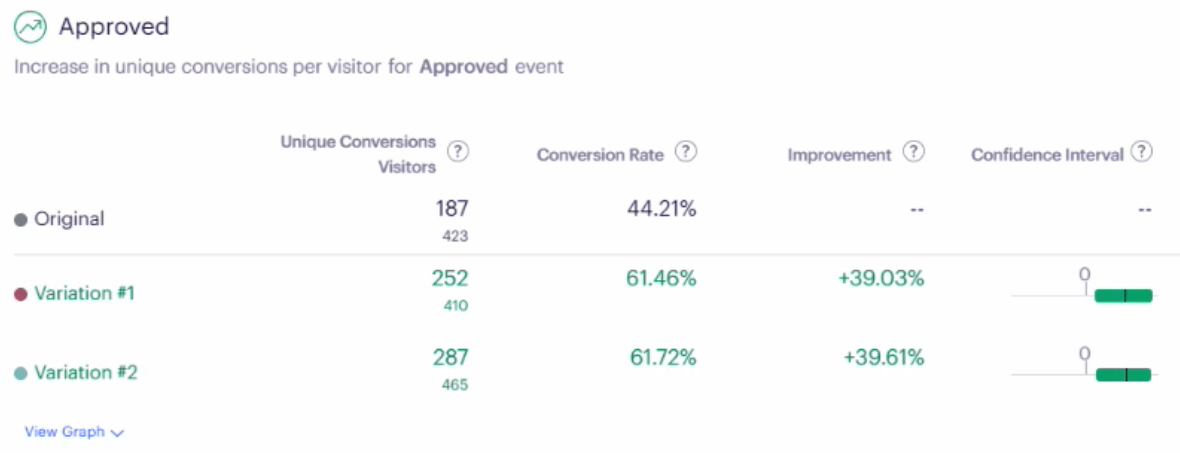
    Optimizely

     

    그렇다면 하위군 분석의 결과를 왜 신뢰할 수 없는지에 대한 이유 몇가지를 간략하게 기술하자면 다음과 같다:

    • 다중 검정을 통해서 FWER이 증가할 수 있다.
    • 각 하위군에서는 무작위배정이 수행되지 않았다.
    • 각 하위군의 표본크기는 전체에 비해 적어져 검정력이 낮아진다.

     

    (b) Causal Segment Analysis (확증적 하위군 분석)

    다음으로 확증적 하위군 분석이란, 특정 하위군에서 얻은 결과를 인과적인 결과로 받아들이고자 하는 경우를 의미한다.

    위와 같은 목적의 하위군 분석은 과거의 실험 등을 바탕으로 특정한 하위군에서의 기능(treatment)의 효과가 전체 집단과 매우 다를 것이라는 충분한 사전 증거가 있는 경우에 수행될 수 있다.

    단, 이를 위해서는 분석할 하위군을 실험의 기획단계에서 명시적으로 정의해야 한다. 이러한 실험에서는 층화 무작위배정 (stratified randomization)을 바탕으로 실험이 진행되고, 실험의 분석 단계에서 앞서 살펴본 Bonferroni 등의 통계적 유의수준 보정 방법을 적용하게 된다. 이러한 확증적 하위군 분석은 우선 사내에 실험 문화가 정착된 다음, User experience funnel 에서 단계별로 최적화 하고 싶은 니즈가 발생할 경우 수행되는 것이 일반적이다.

     

    정리하자면, 대부분의 하위군 분석은 인사이트를 얻기 위한 탐색적 분석의 성격을 띄기 때문에 다중 검정에 대한 별다른 보정 작업이 필요하지 않으며, 따라서 그 결과를 인과적으로 받아들이지 않는 것에 대한 각별한 주의가 필요하다.

    가령, 하위군 분석의 결과로 새로운 기능이 여성 그룹에서는 유의하지 않고 남성 그룹에서만 유의했을 경우, 해당 결과는 어디까지나 인사이트를 얻기 위한 참고 자료로만 활용되어야 한다. 만약 실제로 성별에 따라 효과에 차이가 있는지에 관심이 있는 경우에는 primary metric을 성별별 지표로 삼는 별도의 follow-up experiment를 진행해야 한다.

     

    2.2. 일반적인 주의 사항들

    해당 아티클에는 하위군 분석의 수행과 관련한 일반적인 주의 사항 몇가지가 언급되어 있다.

    1. 하위군 분석은 다중검정의 일종이므로 type I error가 증가한다.
    2. 1종 오류를 최소화하기 위해서 필요 최소한으로 “관련이 있는” 하위군만을 선정하라.
    3. Cherry-picking 을 방지하기 위해 어떤 하위군을 분석할지를 사전 실험 계획서에 명시하라. (Pre-registration)
    4. Bonferroni 방법 등의 유의 수준에 대한 보정을 적용하라.
    5. 실험 기간을 최소 두배 이상으로 설정하라 (참고)
    6. 이미 진행된 실험에서의 하위군 분석은 인사이트를 얻는 보조 수단으로만 활용해야 한다. 만약 확증적 결과를 얻고 싶다면 follow-up test를 진행하라 (관련 내용).

     

    3. A/B/n 실험

    실험하고자 하는 대상 (i.e. variant) 이 여러개인 A/B/n 실험의 경우, 1차 유효성 평가변수에 대한 가설 검정은 확증적 분석이기에 다중성에 대한 보정이 필요하다. 이와 관련해 물론 Bonferroni 방법을 사용할 수는 있으나, 이전 포스트에서 살펴본 것처럼 이는 상당히 보수적인 방법이기 때문에 검정력을 손해보게 된다.

    이에 대한 대안으로 임상 통계 분야에서 활용되는 fixed-sequence testing procedure 의 아이디어를 적용해볼 수 있다.

    가령 control, variant1, variant2 로 구성된 실험에서 variant1, variant2 모두 control에 비해 유의미한 차이가 없다는 결론이 도출되었다고 가정해보자. 이 경우 당연하게도, variant1, variant2 간의 비교는 크게 의미가 없을 것이다. 왜냐하면 애당초 귀무가설이 기각되지 못했다는 것은 두 variant 중 어느 것도 control에 비해 성능이 좋지 못했다는 것인데, 이러한 상황에서 variant1과 variant2 간에 우열을 가리는 것은 큰 의미가 없기 때문이다. 물론 배움의 측면에서 두 variant 간 우열을 판단하는 것이 필요할 수도 있겠으나, 이에 들어가는 비용(유의 수준의 감소)에 비해 값어치가 있는지는 고민해 볼 여지가 있다.

    이러한 맥락에서, 만약 variant1과 variant2 간에 비교가 필요한 상황을 “두 그룹이 모두 control에 비해 효과가 있는 경우”에 한정시키는 경우, 가설 검정의 순서가 고정된 fixed-sequence 방법을 이용해서 최대한의 유의 수준 아래에서 다중성을 보정한 정확한 결과 도출이 가능하다.

    즉, variant 간의 비교가 진행되기 위해서는 우선적으로 각각을 control과 비교한 첫번째 단계의 귀무가설들이 기각되는 것이 선행되어야 한다. 이를 Graphical Notation을 이용해서 도식화하면 다음과 같다.



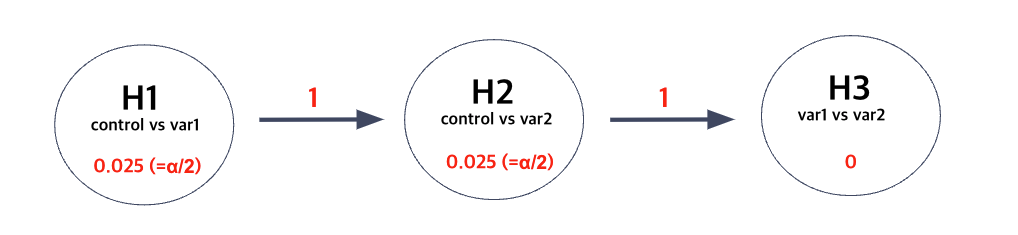
    Fixed Sequence Testing Method

     

    요약하자면, 위 방법은 앞 단계부터 순서대로 가설 검정을 진행 한 다음, 만약 그 결과가 “유의할 경우” (i.e. p-value < $\alpha$) 해당 단계에서 사용된 유의수준을 다음 단계의 가설 검정에 넘겨주는 방식으로 진행된다. 이를 Fall-back procedure (FBP) 라고 부른다.

    위 예시를 바탕으로 FBP의 과정을 구체적으로 뜯어보자면, 우선 control과 variant 간의 비교에서는 일반적인 Bonferroni 방법과 동일한 유의수준인 $0.025$가 각 가설에 배정된다. 그리고 만약 첫번째 가설인 “variant 1과 control 간에 차이가 없다”가 $0.025$의 유의수준 아래에서 기각되었을 경우, 다음 단계의 가설인 “control vs variant 2”는 $0.025$의 유의수준 아래에서 이뤄진다. 한편, 만약 첫번째 가설이 기각되지 않았을 경우, 해당 유의수준인 $0.025$가 다음 단계로 전달되어서 “control vs variant 2”의 가설 검정이 $0.05$ $(= 0.025 + 0.025)$의 유의수준 아래에서 수행된다.

    위 과정을 pseudo code로 표현하면 다음과 같다:


    Pseudo Algorithm of the Fallback Procedure

     

    이 때 알고리즘의 리턴값 $R$은 “기각된” 가설들, 즉 통계적으로 유의하다고 판단된 가설들이다. 이를 바탕으로 family-wise type I error를 사전에 설정된 유의수준 이하로 통제하면서도 variation1 과 variation2 간에 어떤 것이 더 좋은지에 대한 확증적 결과를 얻을 수 있다.

    위 예시에서는 variant가 단 두개 밖에 없었지만, 이를 $N$개로 확장시키는 것도 당연히 가능하다. 단, 이렇게 되면 개별적인 가설에 배정되는 유의수준이 $N$에 비례해서 감소하기 때문에 가급적이면 너무 많은 variant를 두는 것은 지양해야 한다.


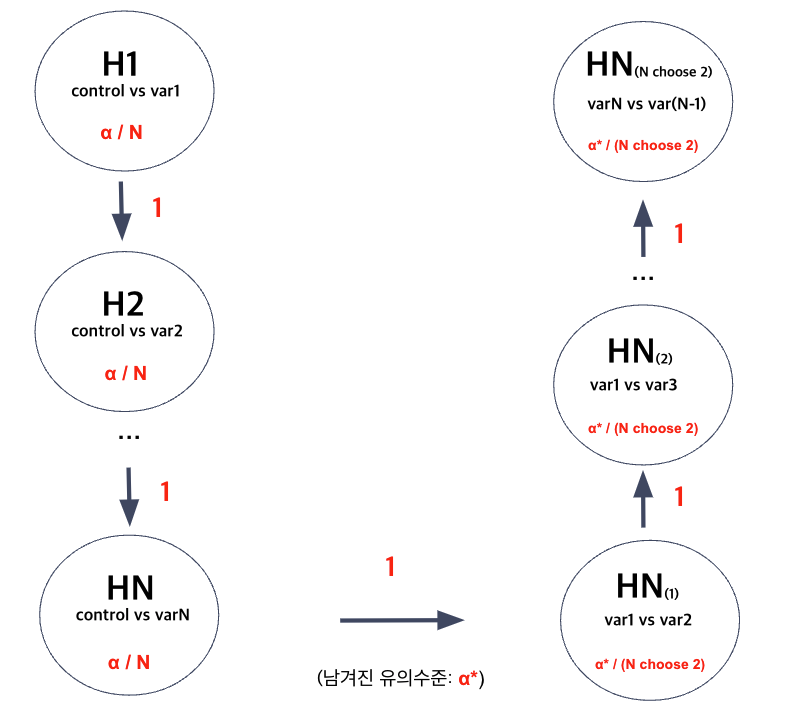
    variant가 총 N개인 경우의 Fallback Procedure

     

    원래 Early stopping과 관련한 내용도 다루려 했으나.. 생각보다 내용이 길어져 이는 별도의 포스트에 따로 정리하도록 하겠다.

     

    Reference

    # ab-test # multiple-testing # segment-analysis # fallback-procedure

    You might also enjoy

    [Survival Analysis] Introduction

    [Outlier Analysis] Outlier Ensembles

    [Outlier Analysis] High-dimensional Outlier Detection

    [Outlier Analysis] Probabilistic and Statistical Models