[A/B Test] 베이지안 A/B Test
해당 포스트에서는 베이지안 방법론을 사용하도록 설계된 A/B Test가 전통적인 빈도주의 (frequentist) 방식에 비해 갖는 몇가지 특징들을 정리해볼 예정이다.
1. 베이지안 A/B Test의 특징
베이지안 방법론의 가장 핵심적인 아이디어는 추정하고자 하는 모수 (parameter) 를 확률 변수라고 생각하는 것이다.
이와 관련해, 빈도주의 통계학에서 p-value가 계산되는 로직을 잠깐 생각해보자면, 이는 “특정한 한 번의 시점“에서 관측된 데이터가 이론적인 확률 분포로부터 얼마나 그럴싸 한 값인지를 확률값으로 나타낸 것이다.
즉, p-value는 본질적으로 그 정의로부터 고정된 한 시점의 정보량만이 반영된 값이라고 할 수 있다. 이게 무슨 말이냐면, 완벽히 동일한 셋팅에서 동일한 객체들에 대해 실험을 진행한다고 하더라도 실제로 우리에게 관측되는 데이터는 시점에 따라 약간씩 차이가 있을 것이기 때문에 이를 바탕으로 계산되는 p-value는 조금씩 다를 것이라는 점이다. 따라서 빈도주의 방식에서는 “실험을 여러번 반복했을 때 잘못된 결과를 내리는 비율의 정도 (i.e. 1종 오류)” 등과 같은 “상대적” 오류가 주된 관심사이다.
그렇다면 베이지안은 어떨까?
베이지안 방법론에서는 “확률 변수”에 대한 통계적 추정 및 검정을 진행하게 된다. 이는 빈도주의와는 다르게 주어진 데이터를 바탕으로 “구체적인 하나의 모수값”을 추정하겠다는 것이 아니라, “해당 모수를 발생시키는 내재된 확률 과정 (i.e. 통계 분포)” 을 추정하려는 것이다. 이러한 맥락에서 베이지안 방법론에서는 “사후분포 (posterior distribution)” 라고 불리는 확률 분포의 형태로 결과가 도출된다.
그 결과로 베이지안 방식에서는 기존의 빈도주의 방식에서 관심이 많던 1종오류 / 2종오류 / 검정력 등의 개념이 상대적으로 덜 중요하게 된다. 그 이유는 앞서 살펴본 것처럼 실험의 결과가 특정한 한 시점에서의 값이 아니라, 이러한 값들이 발생했을 만한 통계 분포이기 때문에 결과 자체에 불확실성이 자연스럽게 고려되기 때문이다.
가령, 베이지안에서는 귀무가설이 맞다는 전제 하에 ~ // 대립가설이 맞다는 전제 하에 ~ 와 같은 방식으로 논의가 전개되지 않는다. 왜냐하면 애당초 귀무가설과 대립가설 각각이 개별적인 통계 분포의 형태로 잡히기 때문에 옳고 그름을 따질 여지가 없기 때문이다. (물론 사후 분포의 형태에 대한 제약 조건이 있는 경우에는 이야기가 조금 달라질 수 있지만, 우리는 중심 극한 정리라는 유용한 도구가 있다.)
그렇기 때문에 베이지안에서는 실험의 결과에 대한 해석 역시 상당히 직관적이게 된다. 예를 들어, 실험의 결과로 아래와 같이 사후 분포가 나오는 경우, A/B Test에 대해 그다지 익숙하지 않은 사람들도 한눈에 주황색 그룹에서 기대수익이 약 200원 정도 높다는 점을 파악할 수 있을 것이다. (통계학에 익숙하지 않은 사람들에게 p-value와 신뢰 구간은 편두통의 주된 원인이다..)
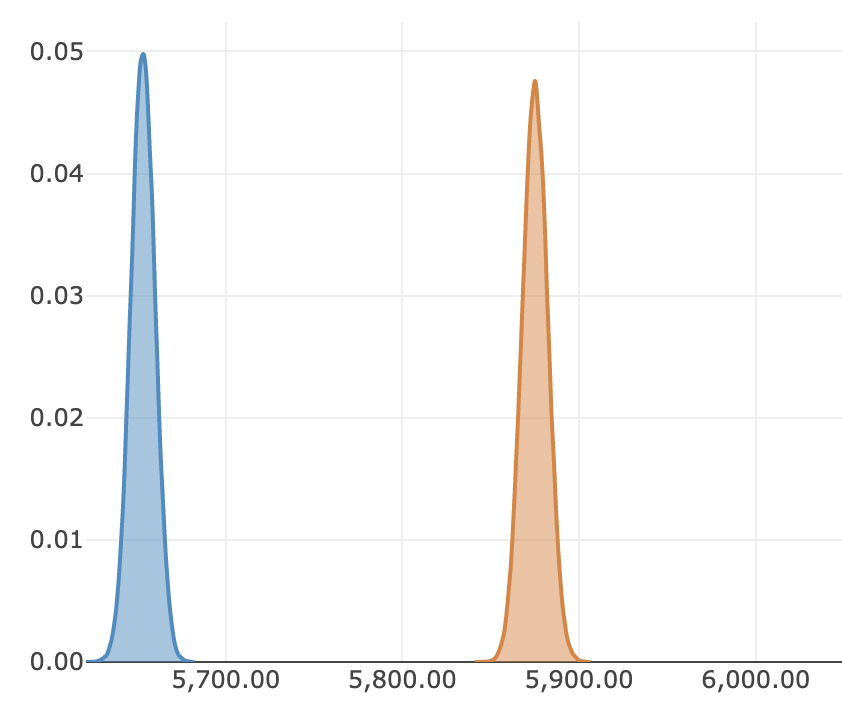
베이지안 A/B Test의 결과 (예시)
이렇듯 베이지안 방법론은 결과 해석의 측면에서 상당히 직관적이고 편리하다는 장점을 갖고 있다.
2. 베이지안 A/B Test의 의사 결정 지표
한편, 베이지안 A/B Test의 주된 비판점 중 하나는 바로 빈도주의 방식의 “p-value”처럼 통일된 의사 결정 기준 (decision rule) 이 확립되지 않아 실험의 결과가 다소 주관적일 수 있다는 점이었다.
그러나 결론부터 말하자면 이는 오해라고 할 수 있다. 베이지안 방법을 이용한 가설 검정 절차에서도 Bayes Factor라는 의사 결정 지표가 분명히 존재하며, 빈도주의의 p-value와 비슷하게 유용한 통계적 성질을 갖고 있다.
Bayes Factor는 수식적으로 다음과 같이 정의된다.
즉, Bayes Factor는 어떠한 데이터가 “대립가설의 분포로부터 나왔을 확률”을 “귀무가설의 분포로부터 나왔을 확률”로 나눈 것으로 정의되는 것을 확인할 수 있는데, 이는 간단하게 말해서 우리에게 주어진 데이터가 (귀무가설에 비해) 대립가설 $H1$을 지지하는 정도를 나타내는 지표라고 이해하면 된다. 이러한 맥락에서 Bayes Factor의 값이 크다는 것은 그만큼 관측된 데이터가 대립가설을 지지한다는 것을 의미하며, 반대로 0에 가까울수록 귀무가설을 지지한다고 해석할 수 있다.
이처럼 베이지안 가설 검정에서는 “이길 확률” 등의 다소 주관적인 지표 이외에도, Bayes Factor를 의사 결정 지표로 활용할 수 있다. 그렇다면 과연 Bayes Factor의 값이 구체적으로 얼마 정도일 때 귀무가설을 기각하게 되는지에 대해 살펴보자.
일반적인 빈도주의 가설 검정에서 유의 수준 $0.05$가 1종 오류를 5% 이내로 컨트롤하는 것과 비슷하게, Bayes Factor는 FDR (False Discovery Rate) 를 컨트롤 할 수 있다는 것이 알려져있다. 구체적으로, 계산된 Bayes Factor의 값이 $K$인 경우 $FDR = 1 / (K+1)$ 이라는 사실이 연구되었다 (참고). 따라서 만약 Bayes Factor의 값이 19인 경우 FDR의 상한선은 5%가 된다. 일반적으로 Bayes Factor가 100을 넘어갈 경우 이는 대립가설에 대한 상당한 증거라고 판단된다.
3. 베이지안 방법론의 장점
3.1. Continuous Monitoring
앞서 살펴본 “결과 해석의 직관성”이라는 측면 이외에도, A/B Test에서 빈도주의 대비 베이지안 방식이 갖는 명확한 장점 중 하나는 바로 continuous monitoring (early stopping)에 대한 이슈가 부분적으로 해소될 수 있다는 점이다.
A/B Test에서 “early stopping” 은 실험을 중도에 종료시키는 것을 의미한다. 예를 들어, 어떠한 실험이 진행되는 과정에서 유저들의 이탈율이 지속적으로 증가하는 것이 발견되었다고 해보자. 이러한 경우, 유저들의 부정적 경험을 최소화하기 위해 실험을 조기에 종료해야할 필요가 있다. 혹은 가령 약 절반 정도 진행된 실험에서 한눈에 보더라도 비교군에서의 효과가 대조군보다 더 큰 것이 확인되었다고 해보자. 이렇게 결과가 매우 명백한 것처럼 보이는 실험의 경우에 대해서도 추가적인 비용을 줄이기 위해 실험을 조기에 종료하고 싶은 니즈가 발생할 수 있다.
하지만 전통적인 빈도주의 방식에서는 이렇게 실험을 조기 종료할 경우 실험의 결과가 왜곡될 우려가 있기 때문에 이는 그리 간단한 문제가 아니다. 해당 내용에 대해서는 해당 포스트에서 자세히 다룬 바 있다.
이와 관련해서 해당 논문의 저자들은 Bayes Factor를 의사 결정 지표로 설계된 베이지안 가설 검정에서는 몇가지의 mild한 조건이 만족된다면 실험을 조기 종료하는 것에 문제가 발생하지 않는다는 점을 수학적으로 도출했다. 구체적인 내용이 궁금하다면 해당 논문을 읽어보는 것을 추천한다.
3.2. Multiple Testing
이와 비슷한 맥락에서, 베이지안 방법론이 갖는 또 하나의 장점은 바로 빈도주의 가설 검정에서 이슈가 되는 다중 검정 문제가 자연스레 해결될 수 있다는 점이다. 다중 검정이란, 하나의 실험에서 여러번의 가설 검정을 수행할 경우 1종 오류가 이론적으로 보장된 유의 수준보다 더 커질 수 있다는 내용인데, 이에 대한 구체적인 내용은 해당 포스트를 참고하기 바란다.
이에 대한 실마리는 베이지안 방법론에서 모수가 추정되는 과정을 잘 뜯어보면 발견할 수 있는데, 관련해서 해당 논문에 제시된 아이디어를 간략히 살펴보도록 하겠다. 해당 내용은 베이지안 통계학에 대한 배경 지식이 있다는 것을 전제로 하므로, 만약 베이지안 통계학이 낯설다면 해당 포스트 시리즈의 1, 2 번째 포스트를 살펴보고 돌아오기를 추천한다.
베이지안 방법론에서 모수는 베이즈 정리라는 공식을 이용해 추론된다. 이 때, 데이터와 사전 지식에 대한 분포 (likelihood & prior) 가 특정한 형태를 만족하는 경우를 conjugate relationship이라고 정의하고, 이러한 경우에 대해서는 사후 분포(posterior)가 closed-form으로 정의된다.
자 그렇다면 이렇게 구해진 사후 분포의 의미를 구체적으로 뜯어보자. 사후 분포란 데이터를 바탕으로 업데이트 된 모수의 분포이며, 가설 검정에서 우리는 개별적인 가설 검정 (e.g. primary metric, secondary metric, guardrail metric, …) 각각에 대한 모수를 (분포의 형태로) 추론하고 싶은 것이다. 이러한 맥락에서 우리는 베이지안 계층 모형 (Bayesian Hierarchical Models) 을 바탕으로 모든 가설을 아우르는 하나의 사후 분포를 정의할 수 있다. 즉, 사후 분포는 결합확률분포 (joint distribution) 의 형태로 정의된다.
한편, 우리가 수행하고자 하는 가설 검정은 궁극적으로 개별적인 가설 검정들에 대한 분포, 즉 앞서 구한 joint posterior를 개별적인 가설의 모수로 적분 (integrate out) 한 “marginal posterior” 를 바탕으로 수행된다. 여기서 주의할 점은 바로 개별적인 가설들에 대한 사후 분포가 두 가설 전부를 포함한 공통의 결합확률분포를 바탕으로 추정된다는 점이다. 그렇기 때문에 여러 지표들에 대해 정의된 가설 검정에 대한 사후 분포는 본질적으로 서로 독립이 아니다. 왜냐하면 애당초 각각의 marginal posterior가 동일한 분포로부터 파생되어 나왔기 때문이다.
이러한 맥락에서 다중 검정의 의미를 다시 한번 되새겨보자. 빈도주의 검정 방법은 개별적인 가설들이 (hypothesis set) 서로 독립이라는 가정 아래 수행된다. 하지만 실제 가설 검정에서 개별적인 가설들은 서로 독립이 아닐 수 있다. 간단한 예시로 새로운 UI에 대한 A/B Test를 수행한다고 할 때, 1차 유효성 평가변수 (primary metric) 에 대한 시험군에서의 효과가 유의했을 경우 나머지 보조 변수들에 대해서도 시험군에서 효과가 유의할 가능성이 높을 수 있다는 점을 자연스레 생각해볼 수 있다.
이처럼 실제로는 독립이 아닌 개별적인 가설 검정들을 여러번 연속해서 수행할 경우 1종 오류가 실제보다 늘어나는 다중 검정의 문제점이 발생하게 된다. 그리고 빈도주의 방식에서 이러한 문제를 해결하는 일반적인 방법은 Bonferroni 방법 등을 바탕으로 1종 오류에 대한 유의 수준을 통계적으로 보정하는 것이다.
하지만 앞서 살펴본 “계층적 모형을 바탕으로 하는” 베이지안 방법론에서는 이런 걱정이 사라진다. 왜냐하면 애당초 두 가설이 서로 독립이어야 한다는 가정 자체가 없기 때문이다. 실제로 각 가설들에 대한 marginal posterior 에서는 다른 가설들의 정보량이 공통의 joint posterior를 통해 반영이 된다는 것을 앞서 살펴보았다. 이러한 측면에서 베이지안의 계층 모형을 통해 모수를 추정할 경우 빈도주의 방식에서 큰 문제가 되는 다중 검정에 대한 문제점이 해소될 수 있다.
4. 베이지안 방법론의 문제점
당연하게도 꽁짜 점심은 없듯이 베이지안 방법론에도 몇가지 문제점이 있다.
이와 관련해서, 개인적으로 생각하는 가장 크리티컬한 문제점은 만약 데이터에 대한 분포가정 (i.e. likelihood) 이 타당하지 않을 경우 “잘못된 사후분포”가 도출될 수 있다는 점이다. 물론 베이지안 통계학의 일반적인 맥락에서 우리는 유연하게 사전 정보와 데이터의 형태를 고려할 수 있다는 점이 이론적으로는 타당하나, 실제 대부분의 상황에서는 계산의 편의를 위해 conjugate relationship을 갖는 다소 제한적인 형태의 분포들이 사용되기 때문이다. 그도 그럴것이 샘플 사이즈가 수십만, 많으면 수백만까지 늘어나는 모수에 대해 MCMC 방법론을 적용하는 것은 현실적으로 무리가 있을 것이다.
또한 베이지안 A/B Test와 관련한 많은 use-case들에서 정의된 사후 분포에 대한 model evaluation 과정이 부재한다는 점도 큰 문제점이라고 생각한다. 만약 conjugate relationship을 사용할 경우, 추정된 사후 분포는 특정한 확률 분포로 그 형태가 고정된다. 물론 우리는 중심 극한 정리가 있기 때문에 모평균에 대한 검정에서는 어느 정도 근사적으로 정규성이 보장될 것이라고 생각해볼 수는 있으나, 실제 유저 데이터는 그 왜도 (skewness) 가 상당하다는 점에서 중심 극한 정리로 인한 정규 근사에 필요한 샘플 사이즈가 무지막지하게 커진다는 문제가 있다.
이러한 맥락에서 베이즈 정리를 바탕으로 사후 분포가 도출된다 하더라도, 해당 사후 분포가 타당한지 아닌지를 판단하는 절차가 없으면 애당초 상한 식재료를 가지고 요리를 하는 상황이 발생할 수 있다. 일반적으로 베이지안 통계학에서는 사후 분포를 진단하기 위해 이로부터 “posterior predictive sample”을 발생시켜 loss와 같은 평가 지표를 계산하는 절차를 거치게 된다. 하지만 이러한 방법은 베이지안 통계학을 어느 정도 공부한 사람이 아닌 이상 접근하기가 힘들기 때문에 실제 필드에서 서비스들과 소통의 측면에서 어려움이 발생할 수 있다. 만약 이처럼 실험의 절대적 안정성이 보장될 수 없다면 베이지안 방법론을 실제 필드에서 활용하기에는 어려울 것이다.
이러한 점들을 고려할 때, 베이지안 A/B Test가 기존의 빈도주의 방식의 A/B Test를 완벽히 대체하기를 기대하는 것은 적어도 현 시점에서는 무리가 있을 것이라고 생각한다. 실제로 베이지안 방법론이 선호되는 큰 이유 중 하나인 불확실성을 구체적으로 수치화 할 수 있다는 장점도 샘플 사이즈가 굉장히 큰 온라인 실험에서는 크게 부각되지 않을 수 있는데, 이는 데이터의 양에 의해 사후 분포의 분산 (variability) 자체가 굉장히 작아질 수 있기 때문이다. 그럼에도 불구하고 베이지안 방식의 직관적인 프레임워크는 빈도주의 방식에서 가려웠던 부분을 긁어줄 수 있는 좋은 대안이기 때문에 베이지안 A/B Test (가설 검정 방법론) 는 앞으로도 유망한 연구 분야라고 생각한다.
Reference
- A. Deng, J. Lu and S. Chen, “Continuous Monitoring of A/B Tests without Pain: Optional Stopping in Bayesian Testing,” 2016 IEEE International Conference on Data Science and Advanced Analytics (DSAA), 2016, pp. 243-252, doi: 10.1109/DSAA.2016.33.
- Andrew Gelman, Jennifer Hill & Masanao Yajima (2012) Why We (Usually) Don’t Have to Worry About Multiple Comparisons, Journal of Research on Educational Effectiveness, 5:2, 189-211, DOI: 10.1080/19345747.2011.618213
- Gómez Villegas, Miguel A. and Ausin, A.C and González Pérez, Beatriz and Rodríguez-Bernal, María Teresa and Salazar, I. and Sanz San Miguel, Luis (2011) Bayesian Analysis of Multiple Hypothesis Testing with Applications to Microarray Experiments. Communications in statistics. Theory and methods, 40 (13). pp. 2276-2291. ISSN 0361-0926