[A/B Test] Multi-layer Experiments
해당 포스트에서는 여러개의 실험이 동시다발적으로 진행되는 플랫폼에서 (i.e. multi-layer experiments) 효율적으로 무작위 배정을 수행할 수 있는 방법에 대해서 살펴볼 예정이다.
1. Single vs Multi Layer
A/B Test는 특정한 기능의 성과에 대한 인과적인 결론을 내리기 위해서 수행되며, 이를 위해서는 당연하게도 대조군과 시험군의 성질이 “실험하고자 하는 기능”을 제외한 모든 측면에서 비슷해야 한다. 따라서 성공적인 실험 플랫폼을 위해서는 여러개의 실험이 동시에 진행되더라도 각 실험들이 서로에게 영향을 미치지 않고 실험 간 독립성이 보장되어야만 하는데, 결국 이는 실험에 참여하는 유저들을 임의로 나누어 놓은 “버켓”의 퀄리티와 직접적인 연관이 있다.
이러한 맥락에서 “multi-layer experiment platform”이란, 동일한 유저들(모수)을 여러 실험들에서 중복해 사용할 수 있도록 설계된 실험 플랫폼을 의미한다. 만약 실험에 가용될 수 있는 전체 유저 수가 10만명이며 동시에 두개의 실험을 진행한다고 할 때, multi-layer experiment platform에서는 매 실험마다 10만명의 표본을 전부 활용할 수 있다.
한편, 이와는 반대로 “single-layer experiment platform”에서는 동시에 진행되는 두개의 실험에 대해 각각 5만명씩의 유저가 할당된다. 즉, multi-layer experiment platform에 비해 각 실험마다 약 절반 정도의 표본 크기를 손해보게되는 것이다.
각각에 대해서 좀 더 구체적으로 살펴보자.
Single-layer Experiment Platform
설명의 편의를 위해, 총 $N=10000$ 의 모집단 크기와 대조군 시험군 각각에 절반의 샘플이 할당되는 (i.e. 50/50 split) 서로 다른 두개의 실험 $P_1, P_2$ 가 있다고 가정하겠다. 만약 해당 실험에서 모든 표본을 사용한다고 할 때, single-layer experiment platform에서 각 실험 집단별 버켓 $B$ 의 크기는 다음과 같다.
즉 실험이 두개이므로 각 실험에 5천명씩의 표본이 할당되었으며, 각 실험 내에서 또 다시 대조군과 시험군의 두 그룹으로 나뉘기 때문에 최종적으로 각 버켓에는 2500명의 유저가 배정되는 것이다.
이러한 실험 플랫폼 디자인의 장단점은 다음과 같다.
<장점>
- 쉽고 간단하다.
- 모든 실험은 각각 독립적인 버켓(샘플)을 바탕으로 수행되기 때문에, 각 실험 간에 교호 작용 (interaction) 이 발생하지 않는다.
<단점>
- 버켓별 표본의 크기가 줄어든다 (실험의 개수에 따라서 각 버켓에 할당되는 표본수가 linear하게 감소).
- 버켓의 개수가 충분하지 않을 경우, 동시에 여러개의 실험을 진행할 수 없다.
Multi-layer Experiment Platform
한편, 이러한 단점을 보완하기 위해서 전체 모집단(population)이 여러 실험에 동시에 활용되도록 실험 플랫폼을 설계할 수 있다. 하루에도 수백, 수천개의 A/B Test가 동시에 진행되는 구글과 마이크로소프트, 페이스북 등의 플랫폼들이 그 예시라고 할 수 있다.
앞서 살펴본 예시에서, multi-lyaer experiment platform의 경우 각 실험 집단별 버켓 $B$ 의 크기는 다음과 같다.
즉, single-layer design에 비해 각 버켓에 할당되는 표본 수가 두배로 늘어났으며, 늘어난 표본 크기에 대응해서 실험의 검정력이 역시 증가할 것임을 알 수 있다.
하지만 위와 같은 multi-layer experiment platform에서는 한 가지 중요한 이슈가 발생하는데, 이는 바로 동일한 유저들이 서로 다른 실험에 동시에 참여하기 때문에 실험 간 교호 작용 (interaction effect) 이 발생할 수 있다는 점이다.
만약 이처럼 각 실험에서 사용되는 표본(버켓)들이 서로 독립이 아닐 경우 이는 통계적으로 bias를 발생시켜 실험의 결과를 왜곡시킬 우려가 있다. 가령, 만약 첫번째 실험에서 대조군에 배정된 유저들이 두번째 실험에서도 대조군에 배정될 가능성이 높아진다면 A/B Test 필수 요소인 무작위 배정의 원칙이 깨지게 된다. 따라서 multi-layer experiment platform에서는 진행되는 실험들의 독립성이 보장될 수 있도록 각별한 주의가 필요하다.
2. Independent Experiments
그렇다면 구체적으로 어떻게 하면 각 실험의 독립성을 보장하면서 유저들을 버켓에 무작위 배정할 수 있을지를 알아보기에 앞서, 각 실험이 서로 “독립”이라는 것의 의미에 대해 잠시 짚고 넘어가도록 하자. 좀 더 자세한 설명은 해당 포스트를 참고하라.
실험이 독립적이라는 것은, 한마디로 특정한 실험의 결과가 다른 실험에 영향을 미치지 않는 것을 의미한다. 설명의 편의를 위해 다음의 상황을 가정하겠다.
- 첫번째 실험 $P_1$ 에서는 기대수익이 $A$ 만큼 증가하고, 두번째 실험 $P_2$ 에서는 기대수익이 $B$ 만큼 증가한다.
- 실험 $P_1$과 $P_2$는 서로 독립이다.
위와 같은 상황에서 실험 $P_1, P_2$에 대해, 버켓의 가능한 모든 조합별 기대수익의 증가량은 다음과 같다:
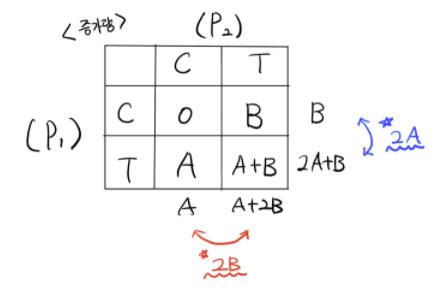
위 표를 바탕으로, 첫번째 실험 $P_1$의 관점에서 기대수익의 증가량 (effect size) 은 $2A + B - B = 2A$로 두번째 실험 $P_2$의 효과 $B$에 의존하지 않는다는 것을 확인할 수 있다 ($P_2$에 대해서도 마찬가지). 따라서 우리는 위 실험에서는 $P_1, P_2$가 서로 독립이라고 결론내릴 수 있는 것이다.
한편, 이와는 반대로 만약 $P_1$의 effect size가 $B$를 포함되게 된다면, 우리는 두 실험간에 교호 작용 (interaction effect) 이 있다고 표현한다. 즉, 첫번째 실험에서의 변경점이 두번째 실험의 변경점으로 인한 효과의 영향을 받아 증가하거나 감소하는 상황을 의미하는 것이다.
Example: Simulation Study
그렇다면 실제로 각 실험이 독립인 경우, 여러개의 실험이 동시에 진행되더라도 통계적으로 bias가 발생하지 않는다는 점을 시뮬레이션 스터디를 바탕으로 파악해보도록 하겠다. 구체적인 내용은 해당 포스트를 참고했으며, 여기서는 간단하게 두개의 실험이 동시에 진행되는 경우에 대한 결과를 살펴볼 예정이다.
시뮬레이션 데이터는 $i$ 번째 실험에서의 유저들의 체류시간 $X_i$ 를 지수 분포로부터 샘플링 했으며, baseline effect size는 대조군과 시험군에 각각에 대해 1과 2로 설정되었다. 또한 이 상황에서 특정한 유저가 treatment를 적용받을 경우 지수 분포의 모수가 1만큼 증가하도록 의도되었다.
위와 같은 세팅에서 10,000 명의 표본에 대해 서로 다른 두개의 실험 $P_1, P_2$을 동시에 진행하는 경우, 개별적인 유저의 관점에서 배정받을 수 있는 모든 버켓(서로 다른 모수를 갖는 지수분포)의 종류는 다음과 같다:
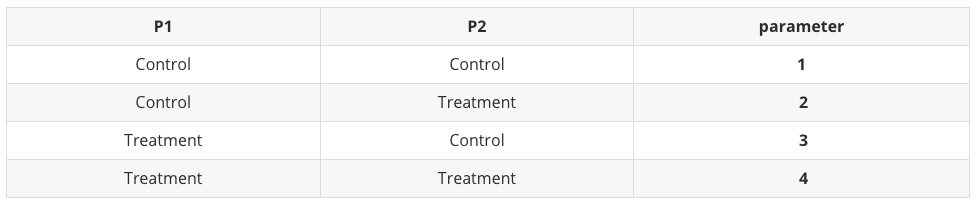
이처럼 실험의 결과로 인해 발생될 수 있는 모수의 종류는 총 4가지이며 각 실험간 교호 작용은 존재하지 않는다고 가정되었다. 또한 결과의 시각화를 위해 위와 같은 4개의 모수를 서로 다른 색깔로 인코딩 했다.
이제 총 10,000명의 개별적인 표본들에 대해서, 50/50 random split을 바탕으로 수행된 독립적인 두 개의 실험에 대한 결과 (모수의 크기 = 색깔) 를 100x100 이미지로 표현해보자. 이 때 각각의 1x1 픽셀은 개별적인 한명의 유저를 의미하게 된다.
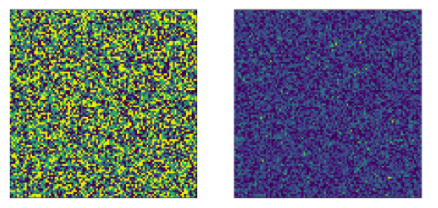
왼쪽의 그림은 각 표본들에 대한 실제 모수 (1,2,3,4 중 한개) 를 의미하며, 오른쪽 그림은 해당 모수를 갖는 지수분포로 부터 샘플링된 값을 의미한다.
이 때 우리가 살펴봐야할 것은 위 그림들에서 모든 색깔이 랜덤하게 분포되어 있는지의 여부인데, 위 그림은 살짝 보기가 불편하므로 두개의 모수 쌍 (1,2 // 3,4) 을 기준으로 재정렬해서 다음과 같이 픽셀들을 재정렬했다.
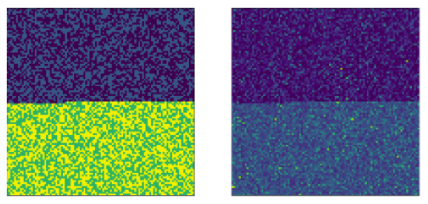
한눈에 봐도 서로 다른 두개의 실험에서 대조군과 시험군이 uniform하게 분포되어 있는 것을 확인할 수 있다. 이는 유저들이 두개의 실험에 동시에 참여했음에도 불구하고, 유저들에 대한 버켓, 즉 각 실험에서의 대조군과 시험군이 모두 독립인 것을 의미한다. 따라서 결론적으로 버켓들의 독립성이 보장되기만 한다면 서로 다른 실험 $P_1$과 $P_2$를 동시에 진행하더라도 무작위 배정의 측면에서 아무런 문제가 발생하지 않음을 확인할 수 있다.
3. Dependent Experiments
한편, 위와는 다르게 만약 각 실험이 서로 독립이 아닐 경우, 즉 실험 간 교호 작용이 있는 경우와 관련한 사례들을 간략하게 살펴보도록 하겠다.
우선 가장 간단하게 생각해볼 수 있는 가능성은, 두 실험에서 테스트하고자 하는 기능 간에 서로 밀접한 연관성이 있어서 시너지 효과를 내는 경우가 있을 수 있다. 예를 들어, 실험 1에서는 특정 웹사이트의 “폰트 크기”를, 실험 2에서는 “폰트 색깔”을 실험하고 있다고 해보자. 이 경우 실험을 진행하는 대상이 “동일한 웹사이트에 대한 폰트”라는 점에서 자연스레 교호작용이 발생할 것이라고 유추해볼 수 있다.
>> e.g. “폰트의 크기가 커짐” + “폰트 색깔이 빨간색” → 더 낮은 전환율 (아마 눈이 아파서..?)
한편, 또 하나의 가능성은 각 실험에 사용되는 “버켓”들이 서로 독립적이지 않은 경우이다. 버켓들이 서로 균등하지 않다는 것은 무작위 배정이 제대로 수행되지 않았음을 의미하는데, 이는 온라인 A/B 테스트에서 bias를 발생시키는 가장 흔한 원인 중 하나이다. 또한 이는 디버깅이 상당히 까다롭기 때문에 A/A Test, SRM (Sample Ratio Mismatch) 등을 통해서 문제가 발생했다는 사실은 알 수 있더라도, 구체적으로 시스템 상 어느 부분이 원인인지를 밝혀내는 것은 상당한 인내심을 필요로 한다.
이와 관련해서 온라인 실험 플랫폼에서 무작위 배정, 즉 버켓 할당 (bucket assignment) 이 수행되는 과정을 구체적으로 살펴보면서 어떻게 하면 multi-lyaer experiment platform에서 문제 없이 실험을 진행할 수 있을지에 대해 알아보도록 하겠다.
4. Randomization Algorithms
Microsoft는 성공적인 실험 플랫폼을 위해서 randomization algorithm이 만족해야할 기본적인 성질들을 다음과 같이 정의하고 있다.
- Assignment of variants to members happens according to the desired split. There should be no bias toward any particular variant (i.e. no sample size ratio mismatch).
- Variant assignment of a single user is deterministic; the user should be assigned to the same variant on each successive visit to the site.
- When multiple experiments are run concurrently, there must be no correlation between experiments. A user’s assignment to a variant in one experiment must have no effect on the probability of being assigned to a variant in any other experiment.
- The algorithm should support monotonic ramp-up, meaning that the percentage of users who see a Treatment can be slowly increased without changing the assignments of users who were already previously assigned to that Treatment.
이중에서도 특히나 세번째 성질인 “실험의 독립성을 보장하는 것”이 상당히 중요하면서도 까다로운 내용이다. 실제로 (곧 살펴볼) 해시 함수를 이용한 무작위 배정 알고리즘이 [1], [2], [4] 의 성질은 잘 만족하더라도 [3]의 성질을 만족하지 못하는 경우가 많다는 것이 연구되었다 (참고). 그렇다면 구체적으로 어떤 방법들이 있는지를 알아보자.
Modulo Approach
Single-layer experiment platform에서의 무작위 배정 방법으로, 유저 아이디의 일정 부분을 짤라서 (e.g. 10으로 나눈 나머지) 해당 나머지 값에 따라 버켓을 할당하는 방법이다.
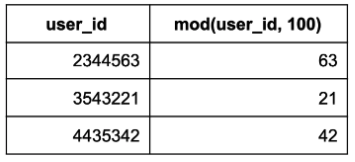
위 예시에 Modulo Approach를 적용할 경우, 유저 아이디를 100 (만들어질 버켓의 개수에 따라 조정) 으로 나눈 나머지를 구한 다음, 이후 진행되는 실험 각각에 버켓의 일정 부분을 할당하는 방식으로 무작위 배정이 수행된다. 즉, 이 방법의 핵심은 버켓을 사전에 미리 나눠놓는 것이다 (위 예시의 경우 총 100개).
구체적인 예시를 하나 들어보겠다. 설명의 편의를 위해 총 16개의 버켓이 있다고 가정할 때, 특정한 하나의 실험에 대해 다음과 같이 버켓을 할당할 수 있다.

그리고 이후 또 다른 실험이 Experiment 1과 동시에 추가적으로 진행될 경우, 아직 사용되지 않은 버켓을 Experiment 2에 배정한다.

단, 이 방법의 문제점은 모든 버켓이 전부 사용되었을 때 나타난다.
만약 위 상황에서 또 하나의 실험 (i.e. Experiment 3) 을 추가적으로 진행하고 싶다고 가정해보자. 이 경우, (각 실험의 효과가 독립이라는 가정 아래) 어쩔 수 없이 이미 다른 실험에서 사용되고 있는 버켓을 재사용할 수 밖에 없으며, 이로 인한 bias를 최소화 하기 위해 Experiment 3에서 대조군과 시험군으로 사용될 버켓을 (0,1,4,5) / (2,3,6,7) 의 버켓으로 설정할 수 있다.
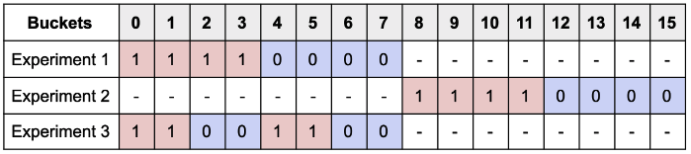
이처럼 Modulo Approach에서 각 버켓은 진행될 실험과 무관하게 사전에 정해지기 때문에, 해당 방식을 사용할 경우 bias가 발생하지 않도록 버켓들을 각 실험에 어떻게 배정하고 관리할지에 대한 많은 고민이 필요하다. 이처럼 Modulo Approach는 동시다발적으로 진행되는 실험의 개수가 많아지면 많아질수록 버켓을 할당하는 과정이 굉장히 복잡해진다는 치명적인 단점을 갖고 있다.
Random Number Generator (RNG) Approach
앞서 살펴본 Modulo approach에서 문제가 발생하는 근본적인 원인은 버켓이 사전에 미리 정해진다는 점이었다.
이에 대한 해결책으로, 각각의 개별적인 실험들마다 버켓을 독립적으로 정의하고, 할당하는 방법을 고려해볼 수 있다. 이처럼 버켓이 매번 랜덤하게 정의된다면 Modulo approach처럼 직접 버켓을 할당하지 않더라도 버켓간의 균질성이 근사적으로 보장될 것임을 직관적으로 생각해볼 수 있다.
그렇다면 어떻게 매 실험마다 버켓을 정의할 수 있을까? 가장 간단한 방법은 random number generator (RNG) 를 사용하는 것이다. 설명의 편의를 위해 다음의 상황을 가정하도록 하겠다:
- 총 10,000개의 population size (유저들은 각각 고유한 아이디로 식별됨)
- 3개의 실험 집단 (variant) : “control” / “variant 1” / “variant 2”
- 각 실험 집단 별로 할당될 샘플 비율: 20 / 40 / 40 (%)
위와 같은 셋팅에서 RNG를 이용해 $2:4:4$ 의 비율을 갖는 버켓을 정의하는 것은 간단하다.
- 각각의 유저에 대해 Uniform(0,1) 에서 임의 난수를 하나 생성
- 생성된 난수값의 범위에 따라 다음과 같이 실험 집단 (버켓) 을 배정
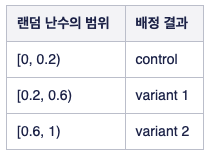
해당 과정을 도식화 하면 다음과 같다.
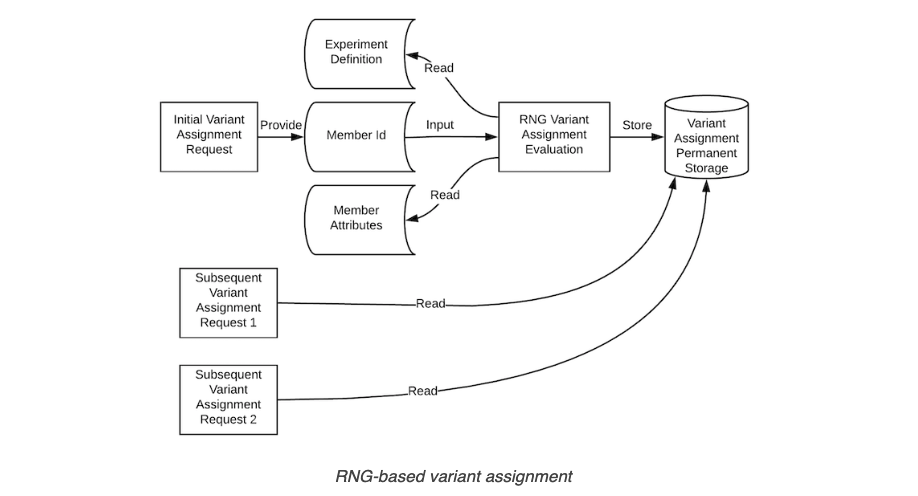
한편, 이 방법 역시 치명적인 문제점이 하나 발생한다. 이는 바로 진행되고 있는 모든 실험에 대해서 유저들의 버켓 할당 정보 (생성된 랜덤 난수) 를 별도의 DB에 저장해둬야 한다는 점이다.
앞서 살펴본 무작위 배정 알고리즘이 만족해야하는 조건들 중 [2]번을 다시 떠올려보자. 각 실험에서 유저들에 대한 버켓 할당은 재현이 가능해야만 한다. 때문에 RNG Approach를 사용할 경우 모든 실험에서의 모든 유저들에 대한 랜덤 난수값을 저장하기 위한 상당한 리소스가 필요하게 되며, 실시간으로 값을 집계하기 위해서 외부 데이터베이스에 저장된 랜덤 난수값을 참조해야하기 때문에 속도가 느려진다는 단점이 있다. 단순히 생각해서 전체 유저가 천만명이라고 할 때, 서로 다른 실험이 10개만 진행되더라도 1억개의 엔트리가 생성될 것이다.
The Hashing Approach
위와 같은 문제점의 대안으로, 대부분의 multi-layer experiment platform에서는 해시 함수를 활용하는 무작위 배정 알고리즘을 채택하고 있다.
해시 함수는 특정한 문자열 (i.e. experiment_name + user_id) 을 uniform한 실수의 공간으로 매핑시켜주는 일대일 함수이며, 특정한 인풋값에 대해 항상 동일한 결과를 반환한다. 따라서 해시 함수만 제대로 정의된다면 앞서 살펴본 RNG Approach처럼 각 실험마다 모든 유저들의 버켓 할당 정보를 일일히 저장할 필요가 없기 때문에 상당한 리소스 절약이 가능해진다는 장점이 있다.
해시 함수를 이용해서 버켓을 생성하는 전체적인 개요는 다음과 같다:
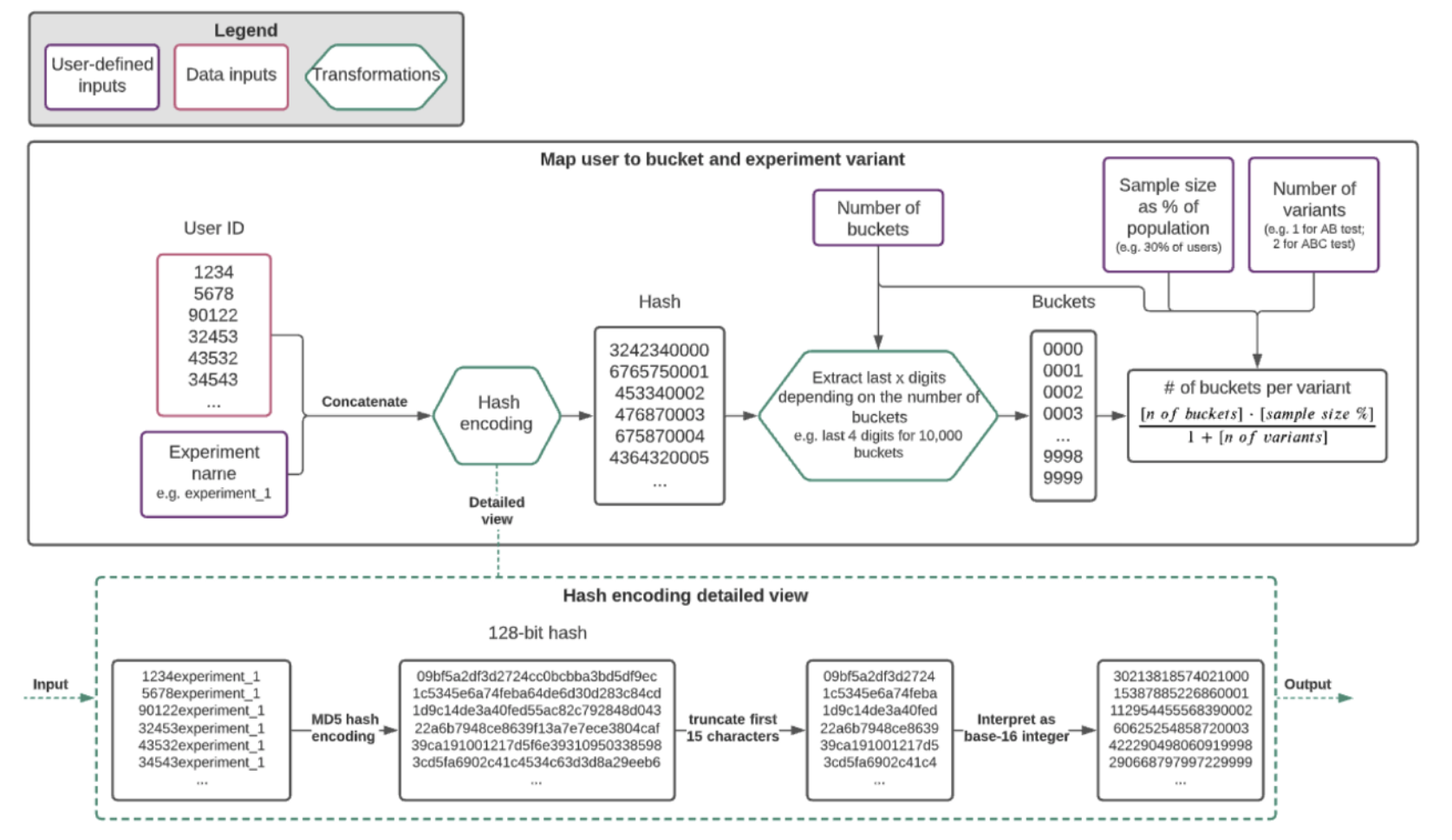
이는 앞서 살펴본 Modulo Approach와는 다르게 매 실험마다 버켓들을 새롭게 정의하는데, 해시 함수를 통해 유저별로 고유한 값을 추출하고, 이를 적절한 값으로 나눈 나머지를 버켓 ID로 갖도록 하는 유저들을 버켓에 할당한다. 그리고 이렇게 생성된 버켓들을 대조군과 시험군의 비율에 맞춰 할당하는 것이다.
한 가지 추가적으로 언급하자면, 앞서 살펴본 조건의 [4]의 맥락에서 일반적으로는 각 실험 집단별로 배정된 버켓의 절반 정도를 남겨두고 ramping 을 사용하도록 설계된다 (아래 그림 참고).
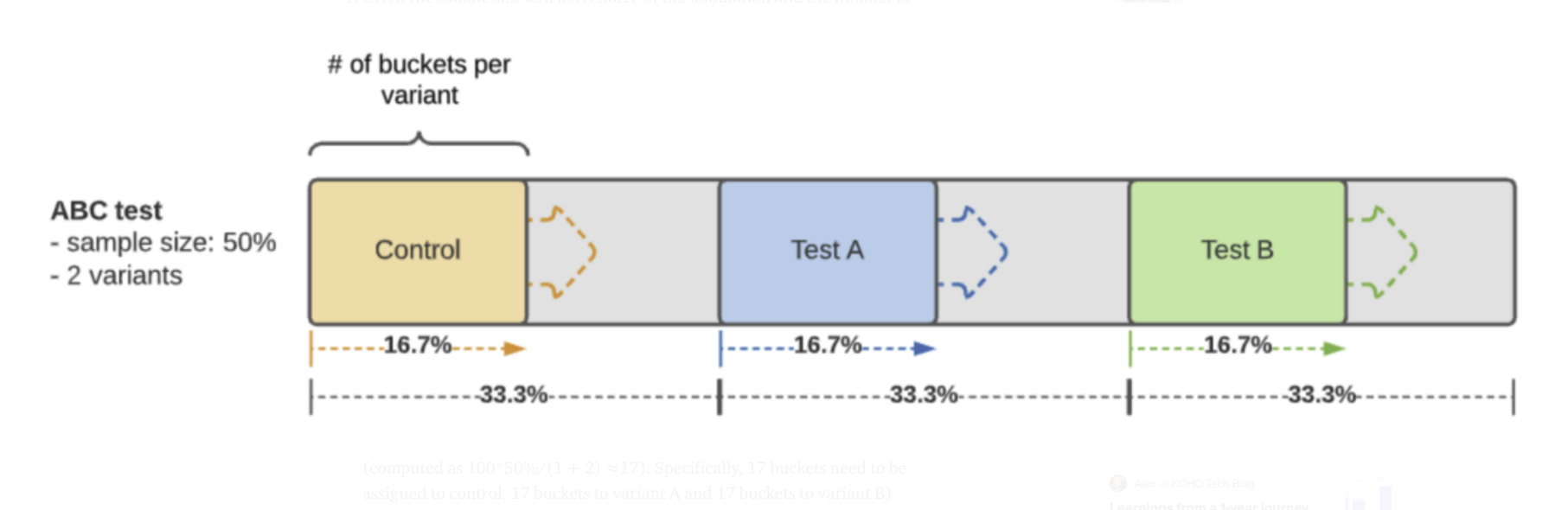
이 때 각 실험 집단별로 사용되는 초기 버켓의 개수는 다음과 같다.
결론적으로, Hashing Approach에서는 여러개의 실험이 동시에 진행되더라도 각 실험마다 버켓이 랜덤하게 생성되기 때문에 동시다발적인 실험들의 교호 작용으로 인한 bias가 일정 수준으로 보정될 것임을 알 수 있다.
한편, 이는 버켓의 생성 과정이 완벽하게 독립적으로 수행된다는 가정을 전제로 깔고 있기 때문에, 해당 방식은 해시 함수의 성능에 크게 의존하게 된다. 이와 관련해서 실제 해시 함수가 제대로 작동하지 않아 실험의 결과에 bias가 발생한 사례가 존재한다 (참고).
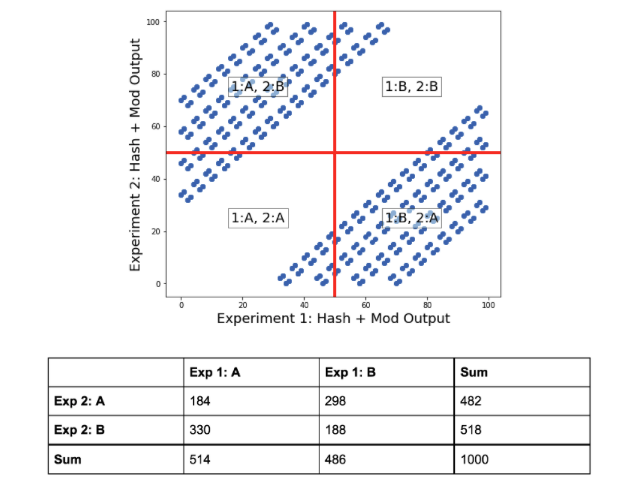
위 사례를 살펴보면 Experiment 1에서 A 그룹에 배정된 사람은 Experiment 2에서 B 그룹에 배정될 가능성이 높은 것을 확인할 수 있는데, 이는 해시 함수가 동시에 진행된 실험들에 대해 독립적인 버켓을 생성하지 못했다는 것을 의미한다. 그리고 이처럼 bias가 있는 버켓을 바탕으로 진행된 A/B Test를 통해서는 의미있는 결론을 도출하기가 어려울 것이다.
이러한 이슈와 관련해서 해당 포스트의 저자들은 여러 해시 함수의 성능을 비교하는 연구를 진행했고, 그 결과 MD5, Murmur3 해시 함수에서는 위 같은 문제가 발생하지 않았다고 한다. 이 밖에도 해시 함수의 성능에 대한 연구는 많은데, 결론적으로 해당 두 해시 함수가 가장 보편적으로 사용되는 것으로 보인다.
Reference
- Detecting and avoiding bucket imbalance in A/B tests
- A/B testing at Linkedin: Assigning variants at scale
- Assign Experiment Variants at Scale in A/B tests: How we imporved the randomized assignment algorithm for online experiments at Wish
- A good hash is hard to find
- A/B Test Bucketing using Hashing