[A/B Test] Interaction effects in experiments

2022, Jul 01

앞서, 여러개의 동시다발적인 실험이 동일한 유저의 모집단을 바탕으로 진행될 수 있도록 설계된 multi-layer experiment의 개념에 대해 살펴보았다. 단 이를 위해서는 한 가지 조건이 만족되어야 했었는데, 이는 바로 실험 간 “interaction effect”가 발생하지 않아야 한다는 점이었다.

이와 관련해서 해당 포스트에서는 실험 간 interaction effect의 존재 여부를 어떻게 발견하고 처리할 수 있을지와 관련해서 간단하게 정리해보도록 하겠다.

1. Definition of Interaction Effects

본격적인 내용으로 들어가기에 앞서 실험 간 interaction effect가 무엇인지에 대한 정의를 살펴보자.

설명의 편의를 위해, 기능 A와 기능 B 중 어떤게 더 높은 수익을 내는지를 비교하기 위한 실험이 있다고 해보자. 이 때, 기능 A을 적용했을 때의 수익 증가율을 $a$, 기능 B에서의 수익 증가율을 $b$ 라고 하겠다. 물론 $a$ 와 $b$ 는 우리가 실험을 통해 추론하고자 하는 모수이기 때문에 실제 참 값을 알 수는 없다.

이러한 맥락에서 해당 값들을 추정하기 위해 기능 A와 B 각각을 대조군과 비교하는 실험을 한번씩 진행했고, 그 결과로 $a$와 $b$에 대해 2%와 5%라는 추정치를 얻었다고 가정하겠다.

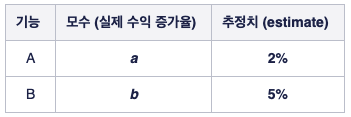
위와 같은 상황에서, 새로운 기능 A를 도입할 경우 수익이 2% 정도 증가하고, B를 도입할 경우 수익이 5% 정도 도입할 것이라고 결론내릴 수 있다.

한편, 만약 기능 A와 B “둘 다”를 도입할 경우에 기대 수익은 어떻게 될까? 이와 관련해서, 만약 두 기능 간 interaction effect가 “없다면”, A와 B를 동시에 적용함으로써 얻을 수 있는 수익의 증가율은 대략 7% 정도가 될 것이라고 추측해볼 수 있다. 반면에, 만약 두 기능간 interaction effect가 “있다면”, 두 기능을 동시에 적용해서 얻을 수 있는 수익의 증가율은 더 이상 7%가 아니게 된다. 만약 양의 상관관계가 있을 경우 수익의 증가율은 7%보다 커지게 될 것이며, 음의 상관관계가 있는 경우 7%보다 감소할 것이다.

<interaction effect X>

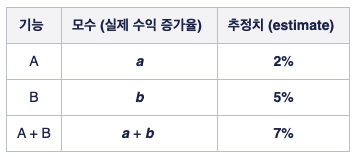
<interaction effect O>

이처럼 interaction effect가 있는 경우 기능 A와 B 모두를 적용받는 유저들의 수익 증가율은 단순히 각 기능에서의 효과 $a, b$ 를 더한 값이 아니게 된다. 더불어 이러한 interaction effect 로 인해 실험의 결과가 왜곡되는 현상이 발생할 수 있게 된다.

이러한 맥락에서 다시 한번 무작위 배정의 중요성이 부각되는데, 그 이유는 만약 무작위 배정이 완벽하게 수행된다면 기능 A, B를 동시에 적용받는 유저들이 대조군과 시험군에 골고루 분포되어 interaction effect로 인한 bias가 전체적으로 보정되기 때문이다. 즉, 무작위 배정만 완벽하다면 우리는 개별적인 실험에서 성능에 대한 비편향추정치 (unbiased estimate)를 얻을 수 있다. (이미지 출처)

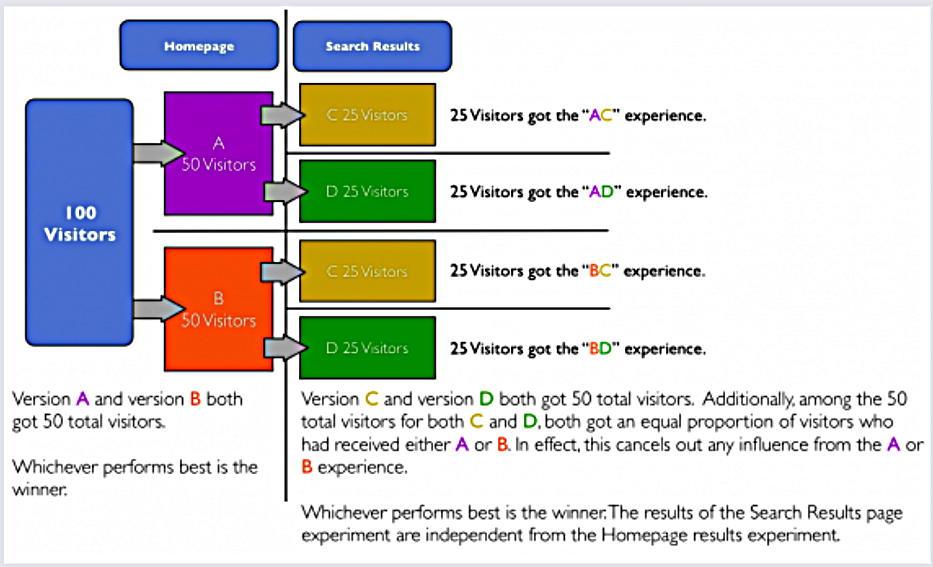
그렇다면 randomization algorithm만 제대로 기능한다면 실험의 결과를 제대로 구할 수 있는데, 굳이 interaction effect를 신경쓸 필요가 있을지에 대한 궁금증이 생길 수 있다. 이와 관련해서 많은 실험 플랫폼들이 interaction effect를 찾아내기 위해 고군분투하는 주된 이유는, 바로 유저의 부정적인 경험을 야기할 수 있는 negative interaction effect를 찾아내기 위함이다.

가령, 페이스북 광고의 “폰트 색깔”과 “배경 색깔”에 대한 실험을 진행한다고 할 때, 만약 특정한 그룹의 유저들이 빨간색 폰트와 빨간색 배경의 조합에 노출될 경우 해당 유저들은 끔찍한 경험을 하게 될 것 이다. 물론 이렇게 직관적으로 예상이 가능한 interaction effect는 사전에 실험의 관리자에 의해 필터링이 될 것이나, 실제로는 어떠한 기능들의 조합이 유저에게 부정적인 경험을 줄지 사전에 알 수 없는 경우가 많기 때문에 어떠한 상황에서 interaction effect가 안 좋은 쪽으로 발생하는지를 미리 규명하고 싶은 니즈가 발생하게 된다.

2. Handling Interaction Effects

그렇다면 실제 실험에서 interaction effect가 존재하는지 여부를 직/간접적으로 파악할 수 있는 몇가지 방법들에 대해 살펴보도록 하자.

Isolating Experiments

사실 당연한 이야기이지만, interaction effect를 방지하기 위한 가장 확실한 방법은 interaction effect 자체가 발생될 수 없도록 실험 플랫폼을 설계하는 것이다. 이를 “isolated experiments”라고 표현하는데, 핵심은 특정 실험에 참가한 유저들이 또 다른 실험에 동시에 참가할 수 없게끔 버켓을 정의하는 것이다 (i.e. single-layer experiments).

단, 이러한 방법은 앞선 포스트에서 살펴본 것처럼 실험이 많아지는 경우 스케일링 문제가 발생한다는 것과 검정력이 낮아진다는 단점 때문에 본질적인 한계점을 갖고 있다. 이와 관련해서 해당 아티클에서는 다음과 같은 어쩔 수 없는 상황을 제외하고는 가급적이면 multi-layer experiment design을 사용할 것을 권고하고 있다.

동일한 유저가 서로 다른 실험에 배정되는 것이 물리적으로 불가능한 경우 (추천 알고리즘 1 vs 추천 알고리즘 2)
유저에게 부정적인 경험을 발생시킬 수 있는 경우
매우 정확한 결과 도출이 필요한 경우

Manual Inspection

여러 실험 플랫폼들에서 경험적으로 발견된 것 중에 하나는, 실제 실험에서 우리가 전혀 예상하지 못한 방향으로 상당한 interaction effect가 발생하는 경우는 매우 드물다는 점이다 (참고).

특히나 유저에게 부정적인 경험을 초래할 만한 interaction effect의 경우는 직관적인 측면에서 미리 예측하고 대응할 수 있는 경우가 많다. 가령 아래와 같은 실험에서 파란색 버튼과 파란색 배경 각각에 대해서는 성능이 좋았다고 하더라도, 만약 두 기능을 동시에 적용할 경우 상당한 문제가 발생할 것이라는 점은 그 누구라도 쉽게 예측할 수 있을 것이다.

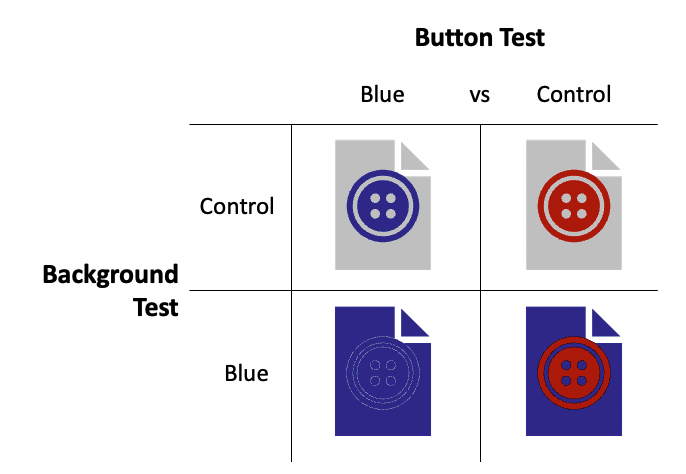
이러한 측면에서 많은 회사들은 실험을 관리하는 별도의 팀 또는 TF를 구성하고 있다. 해당 팀원들은 동시 다발적으로 진행되는 실험들을 관리하고, 새로운 실험에 대한 로드맵을 파악한 다음 어떠한 부분에서 기존에 진행되고 있는 실험들과 충돌이 발생할 수 있는지를 파악하는 업무를 수행하게 된다. 이 과정에서 충돌이 발생할 것 같은 실험들은 별도로 분리 (isolating) 되며, 기존 실험이 끝난 다음 wash-out period를 거친 뒤 진행된다. 이런 식으로 매뉴얼하게 실험들을 관리하는 것을 통해 multi-layer experiment platform의 안정성을 보장하는 것은 많은 플랫폼들의 공통적인 방식이다.

Multi-variate Testing (MVT)

자 이제는 interaction effect을 피해가는 것이 아니라, 이를 발견할 수 있는 방법에 대해서 살펴보자. 가장 간단하게 interaction effect를 찾아낼 수 있는 방법은 다변량 실험(MVT)을 진행하는 것이다.

다변량 실험(MVT)이란, 측정하고자 하는 모든 기능의 조합들을 각각 하나의 variant로 잡은 다음 가설 검정을 수행하는 것으로, 한마디로 표현하자면 variant가 여러개가 있는 실험을 의미한다. 예를 들어, 어떠한 플랫폼에 게시할 광고와 관련해서 “문구”, “배경 색깔”, “폰트 색깔”의 총 3가지 요인에 대한 실험을 진행한다고 해보겠다.

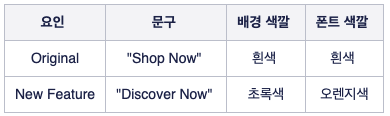
이 때, 실험하고자 하는 3가지 기능에 대한 모든 가능한 조합은 총 8개 이다 (=2x2x2).

>> [“Shop Now” 문구 + 흰색 배경 + 흰색 폰트] // [“Shop Now” 문구 + 초록색 배경 + 흰색 폰트] // … // [“Discover Now” 문구 + 초록색 배경 + 오렌지색 폰트]

이러한 모든 조합을 각각 하나의 variant로 설정한 다음, 각 조합별로 유저들을 무작위 배정한 다음 지표를 계산하게 된다. 위 예시에서는 MVT의 결과로 총 8개의 조합에 대한 개별적인 결과를 얻을 수 있는데, 해당 결과를 바탕으로 interaction effect가 있는지 여부를 판단하기 위해서는 “section rollup” 을 사용할 수 있다.

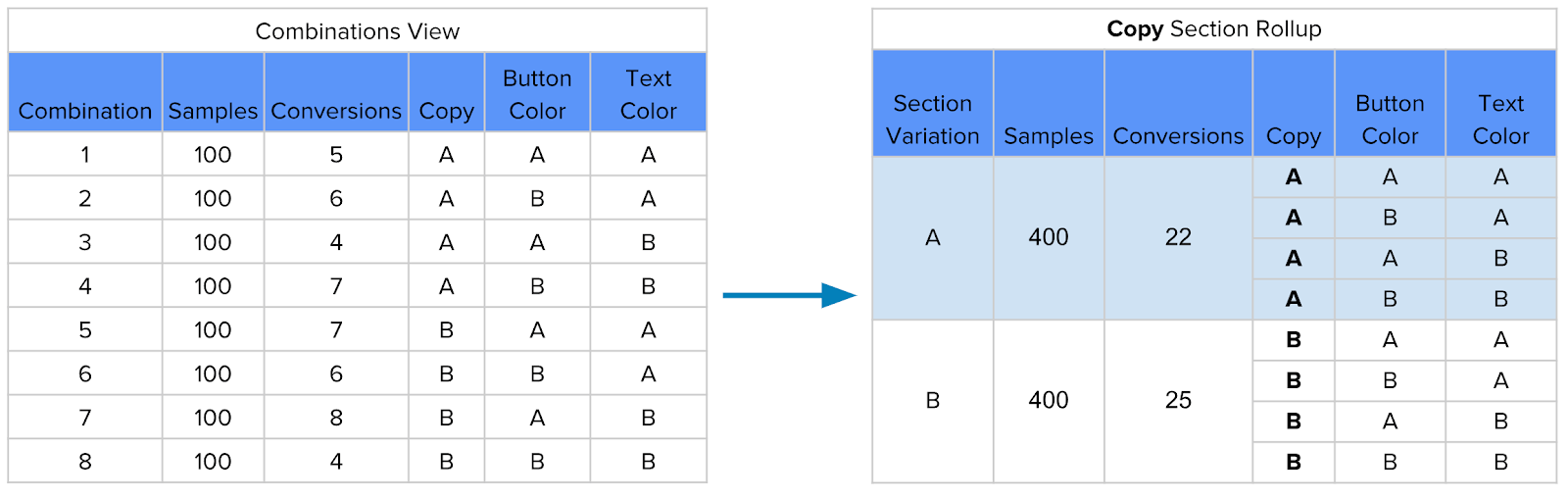
위 표를 보면 section rollup이 무엇인지를 쉽게 이해할 수 있는데, 만약 문구 (Copy) 별로 결과를 집계를 할 경우 (rollup), 해당 결과를 특정한 문구 (A vs B)에 대한 일반적인 A/B Test의 결과로 간주할 수 있게 된다 (오른쪽 표 참고).

이를 바탕으로 특정한 문구 B에 대한 나머지 요인들의 interaction effect를 진단하기 위해서는 문구 B를 기준으로 rollup된 결과를 나머지 요인들에 대한 대조군의 결과와 비교하면 된다.

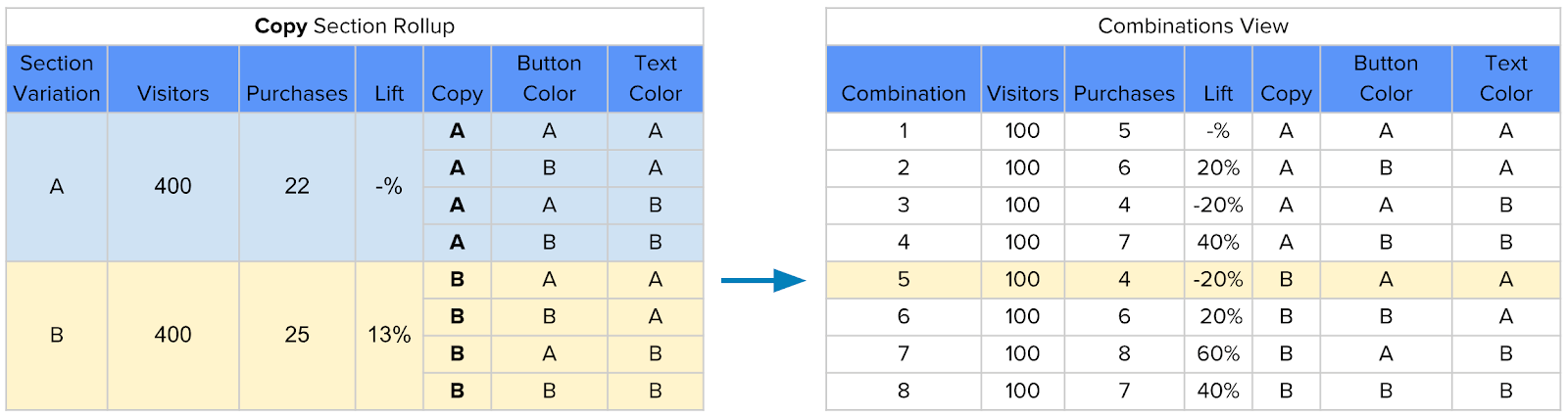
위 표를 바탕으로, 문구 B만이 변경되었을 때의 증가율은 약 -20% 로 안좋은 성능을 보였던 반면, 문구 B가 다른 배경 색깔 및 폰트 색깔과 함께 사용될 경우에는 증가율이 +13% 로 증가한 것을 확인할 수 있다. 이러한 결과의 차이는 바로 문구가 다른 요인들에 대해 (positive 한) interaction effect가 있다는 것에 대한 간접적인 증거가 된다.

반면, 이렇게 MVT를 이용해서 interaction effect를 진단하려는 시도는 두 가지 한계점을 갖고 있다.

첫 번째로는, 해당 방법을 통해서 interaction effect를 잡아낼 수 없는 경우가 존재한다. 가령, 위와 동일한 상황에서 문구 B가 폰트 색깔과 -5%의 interaction effect가 있고, 배경 색깔과는 +5%의 interaction effect가 있다고 할 때, 전체적인 interaction effect는 0%로 없어지는 상황이 발생한다. 그렇기 때문에 이러한 휴리스틱적인 방식은 어디까지나 “간접적인” 증거만을 제시할 수 있다.

두 번째로는, 실험하고자 하는 기능이 많아질 수록 모든 조합을 개별적인 variant로 고려하는 것이 어렵게 된다. 가령 위 예시의 경우 테스트하고자 하는 요인이 3개 밖에 없음에도 불구하고 8개의 조합이 발생하게 되는데, 이보다 요인의 개수가 많아질 수록 기하급수적으로 variant가 늘어나게 된다. 이를 보완하기 위해 가능한 여러 조합 중 일부분을 선택하는 “partial-factorial MVT” 를 고려해볼 수 있다.

ANOVA (Analysis of Variance)

통계적인 측면에서 interaction effect를 파악하는 가장 정석적인 접근법은 ANOVA 모형을 바탕으로 interaction effect가 통계적으로 유의한지를 검정하는 것이다.

앞서 살펴보았던 예시와 유사하게, “폰트의 색깔”과 “배경 색깔”에 대한 실험 상황을 바탕으로 간단하게 (two-way) ANOVA 모형에 대해서 복습해보도록 하겠다. 이 때 우리는 두개의 기능 (A, B) 각각의 성능에 대해서 알아보고 싶으므로, 각 기능을 “블록”으로 하는 테이블의 형태로 실험에서 수집된 데이터를 정렬할 수 있게 된다.

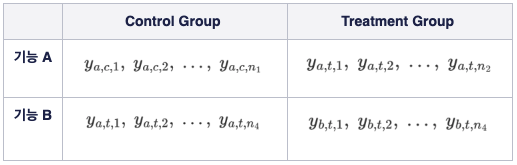
위 테이블에서 각 셀은 해당 그룹의 관측치를 의미하며, subscript는 각각 [기능, 실험집단, 인덱스]를 나타낸다.

이러한 셋팅에서 수행하고자 하는 가설 검정 문제는 다음과 같다.

여기서 한가지 의문점이 들 수 있는데, “interaction effect”을 파악하는 과정에서 왜 갑자기 “평균 차이”에 대한 가설 검정이 진행되고 있는지가 궁금할 수 있다.

이와 관련해 주의할 점은, 물론 ANOVA 모형을 통해 수행하고자 하는 primary hypothesis는 각 그룹 간 “평균 차이”이지만, 대부분의 경우 이에 앞서 blocking factor (위 예시의 기능 A, B) 간 interaction effect가 유의미한지에 대한 가설 검정이 선행된다는 점이다. 그 이유는 만약 interaction effect가 유의하다면 그룹 간 평균 차이의 추정치에 bias가 생기기 때문에 실험의 결과 자체가 무의미해지기 때문이다. 따라서 이러한 ANOVA의 프레임워크를 활용해서 interaction effect가 존재하는지 여부에 대한 통계적 가설 검정을 진행할 수 있다.

참고로, 위와 같은 ANOVA 모형은 우리에게 좀 더 익숙한 선형 회귀 모형 (linear regression) 의 형태로도 표현이 가능하다. 이 경우에 interaction effect에 대한 가설 검정은 회귀 계수 $\beta_3$ 가 0인지 아닌지에 대한 가설 검정과 대응된다.

$$ Y_i = \beta_0 + \beta_1 X_{A,i} + \beta_2 X_{B,i} + \beta_3 X_{A,i}X_{B,i} + \epsilon_i, \quad \epsilon_i \sim N(0, \sigma^2) $$

이러한 셋팅에서 블록 (기능 A, B) 간 interaction effect가 있는지를 검정하기 위해, ANOVA 모형에서는 앞서 살펴본 테이블의 각 셀을 단위로 분산을 쪼갠 다음, 관측치들을 바탕으로 구해진 표본 분산이 이론적 분산에 비해 얼마나 차이가 나는지를 바탕으로 해당 가설을 검정한다.

이러한 작업의 결과로 우리는 아래와 같은 ANOVA 테이블을 얻을 수 있게 된다. 위 예시의 경우, 실험의 대상인 “기능”이 아래 테이블의 “Block (B)”에 해당되고, control/treatment group 배정 여부가 “Group (G)”와 대응된다고 할 수 있다.

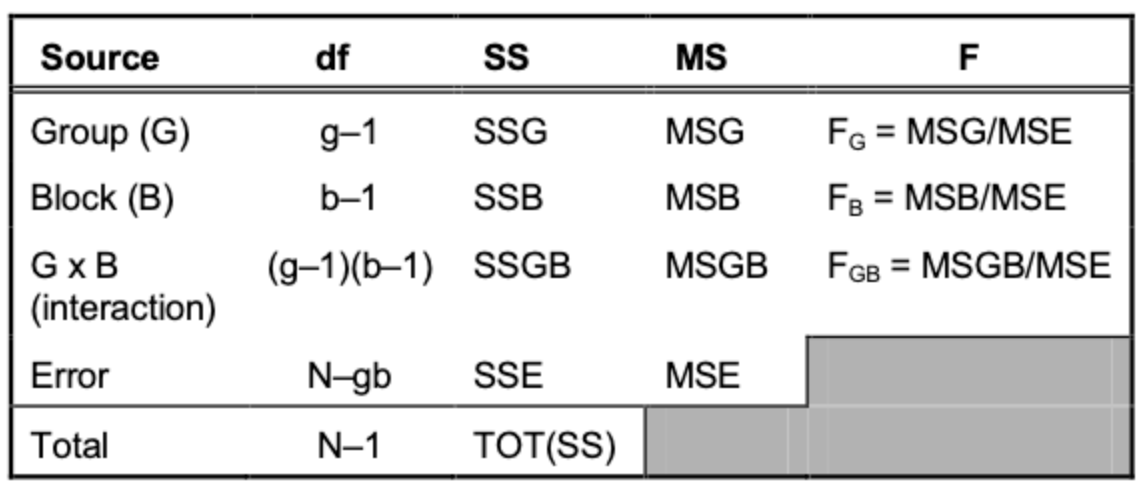
ANOVA Table

위 ANOVA 테이블의 세번째 행인 “G x B”가 우리가 검증하고 싶은 블록(기능 A, B) 간 interaction effect를 대변하며, 만약 해당 값이 통계적으로 0이 아닌 경우 (p-value < 0.05) 우리는 interaction effect가 존재한다고 결론내릴 수 있다. 위와 같은 ANOVA 테이블과 통계적 유의성 결과는 통계 패키지를 이용해서 간단하게 구할 수 있기 때문에 각 항의 구체적인 계산 과정은 생략하도록 하겠다 (파이썬에서는 statsmodel 패키지를 사용하면 된다).

결론적으로, ANOVA 모형을 바탕으로 interaction effect에 대한 통계적 가설 검정을 수행한다는 부분이 여태까지의 핵심이다. 이러한 맥락에서 ANOVA 모형을 활용하면 interaction effect를 가장 정확하게 잡아낼 수 있으나, 실제 진행되고 있는 실험에서 ANOVA를 적용하는 것은 다음의 이유들로 인해 어려울 수 있다.

ANOVA는 실험 집단간 “평균이 같거나 다르다”만을 제시할 뿐이므로 어떠한 variant가 “가장 좋은지”를 보는 것이 목적인 A/B Test와는 결이 다를 수 있다.
negative interaction effect를 찾는 것이 목적인 상황에서 실제로 이러한 interaction effect가 있었는지를 알 수 있는 시점은 실험이 끝난 다음이다.

따라서 “현실적으로” ANOVA 모형을 최대로 활용할 수 있는 방안은 과거에 진행된 실험들에서 어떤 기능끼리의 조합에서 negative interaction effect가 발생했는지를 회고적으로 파악한 다음, 이에 대한 레퍼런스를 만드는 것이다. 애당초 interaction effect를 파악하려는 니즈는 “우리가 예상하지 못했던 조합”을 찾아내려는 것이라는 측면에서, 과거에 경험적으로 어떤 조합들에서 유의미한 interaction이 있었는지에 대한 정보는 실험 관리의 측면에서 유의미한 참고 자료가 될 수 있기 때문이다.

Reference

# ab-test # multi-layer-experiments # interaction-effect

[A/B Test] Interaction effects in experiments

1. Definition of Interaction Effects