[Outlier Analysis] Probabilistic and Statistical Models
컴퓨팅 기술이 고도화됨에 따라 알고리즘적인 접근이 많이 사용되긴 하지만, 그럼에도 불구하고 통계학의 확률적 모형들 역시 지금까지도 이상치 탐지 분야에서 상당히 유용하게 사용된다. 이러한 통계적 방법론들의 기원은 19세기까지 거슬러 올라가는데, 해당 포스트에서는 전통적인 통계적 기법들이 어떻게 이상치 탐지 분야에 자연스레 활용될 수 있는지를 살펴볼 예정이다.
이상치 탐지와 관련해서 가장 많이 쓰이는 통계적 방법론은 extreme univariate test 와 관련이 있다. 얼핏보면 단순히 1차원에서의 이상치 탐지가 뭐 그리 대수냐라고 할 수 있겠으나, 조금만 생각해보면 이는 굉장히 유용하게 활용될 여지가 있다는 사실을 깨달을 수 있다. 가령, 대부분의 이상치 탐지 알고리즘은 각 데이터 인스턴스마다 1개씩 일차원의 outlier score를 반환한다. 이후 이러한 outlier score 들로부터 극단값을 판단한 다음 최종적으로 outlier threshold를 설정하게 되는데, 이 과정에서 자연스럽게 extreme value test가 활용될 수 있다.
물론 이러한 univariate test 이외에도 아예 직접적으로 확률 모형을 이상치 탐지에 활용할 수도 있다. 그 중에서도 특히나 유용한 것은 혼합 모형 (mixture models) 인데, 이는 일종의 “통계적” 클러스터링 기법이라고 볼 수 있다. 이러한 혼합 모형의 큰 장점은 mixture component 만 잘 정의된다면 비교적 다양한 구조의 데이터에 폭넓게 활용될 수 있다는 점이다. 또한 해당 모형은 generative model이기 때문에 자연스럽게 likelihood를 outlier score로 활용할 수 있다.
<목차>
1. Extreme-value analysis for univariate data
2. Extreme-Value Analysis in Multivariate Data using boundary properties
3. Probabilistic Mixture models for outlier analysis
4. Limitations of probabilistic models for outlier analysis
1. Extreme-value analysis for univariate data
통계학에서 이상치에 대한 연구는 특정한 분포에서 꼬리의 성질을 바탕으로 (tail property) 일차원 데이터에서 이상치를 파악하려는 시도로부터 출발했다. 이와 관련해 “extreme-value analysis” 란, 특정한 통계 분포의 분포적 꼬리 (i.e. distribution tail ) 를 규명하려는 작업을 의미한다. 직관적으로, 통계 분포에서 낮은 확률값 (likelihood) 을 갖는 부분은 이상치로 정의하는 것이 자연스러울 것이다.
한편, 실제 상황에서는 데이터의 분포를 가정하는 것이 쉽지 않을 수 있다. 이러한 경우 사용될 수 있는 한가지 유용한 수학적 도구는 바로 “tail inequalities” 인데, 이를 바탕으로 분포의 형태와 무관하게 어떠한 확률 변수의 값이 가질 수 있는 이론적 확률에 대한 범위를 제한시킬 수 있다. 이렇게 얻어진 이론적 boundary를 넘어가는 값들은 정상적인 매커니즘이 아닌 “다른 프로세스”로 부터 발생된 것으로 간주할 수 있으며, 이는 우리가 찾고자 하는 이상치가 된다.
이 과정에서 기본적으로 더 강한 가정이 사용될 수록 더 좁은 (tight 한) 범위로 확률 변수의 값을 제한할 수 있다. 다시 말해, 별다른 가정사항이 없는 inequality의 경우 범용성은 넓을 수 있으나 tail의 bound가 더 넓다는 단점이 있으며, 이와는 반대로 보수적인 tail bound를 잡기 위해서는 좀 더 strong한 condition이 필요하다. 이러한 맥락에서 구체적으로 네 가지의 부등식을 살펴보도록 하겠다.
1.1 Markov Inequality
Markov Inequality 는 가장 general하게 적용될 수 있는 기본적인 tail inequality 인데, 이는 양의 실수에서 정의되는 확률 변수 $X$ 에 대해 평균이 $\mathbb{E}[X]$ 일 경우 어떠한 상수 $\alpha$ 에 대해 다음을 보장한다.
Markov inequality 는 다음의 두가지 가정 사항을 필요로 한다. 두 조건 모두 그렇게 강한 가정 사항은 아니기 때문에 이로부터 얻어지는 tail bound 역시 그렇게 실용적이지는 않다.
- 확률변수 $X$는 음수를 제외한 실수 전체에서 정의된다.
- 1차 적률 (평균) 값이 유한한 값으로 제한 (bounded) 된다.
1.2. Chebychev Inequality
앞서 살펴본 Markov Inequality 는 음수가 아닌 확률 변수에 대해서만 정의될 수 있었다. 이를 좀 더 완화시킨 것이 바로 Chebychev Inequality 인데, 구체적으로 이는 어떠한 확률 변수 $X$ 에 대해 $Y = |X - E[X]|$의 변수 변환을 적용해서 다음과 같이 정의된다.
이와 같이 특정한 확률변수에 non-negative한 함수를 씌워 치역을 음수가 아닌 실수의 영역으로 바꿔준 다음 Markov inequality 를 적용하는 것은 굉장히 유용하게 사용되는 테크닉이다. 곧 살펴볼 Chernoff bound 와 Hoeffding inequality 역시 이러한 아이디어를 바탕으로 정의된다.
현재까지 살펴본 Markov inequality 와 Chebychev inequality 는 상대적으로 약한 부등식이기 때문에 이로 부터 실용적인 결과를 얻기는 힘들 수 있다. 이제 좀 더 강한 조건들을 추가해서 부등식이 제시하는 tail bound를 발전시켜 보도록 하자.
1.3. Chernoff Bound
Chernoff Bound 는 서로 독립인 $N$개의 베르누이 확률변수의 합으로 정의되는 확률변수 $X = \sum_{i=1}^N X_i$ 에 대한 부등식이다. 앞선 부등식들에 비해서 베르누이 분포의 합이라는 좀 더 강한 제약 조건이 붙었다. 조금 특이한 것은 lower tail과 upper tail 각각에 대한 바운더리가 서로 대칭이 아니라는 점이다.
Chernoff Bound 가 적용될 수 있는 가장 대표적인 사례는 제조 공장 등에서의 고장 진단 (fault diagnosis) 이다.
예를 들어, 불량 제품의 발생 확률이 $p$ 인 어떤 생산 공정이 있다고 해보자. 이 때, 이로부터 생산된 $N$개의 제품을 바탕으로 해당 생산 공정이 제대로 작동하고 있는지를 확인해볼 수 있다. 구체적인 적용 과정을 좀 더 살펴보자면, $p=0.01$인 생산 공정에서 총 1000개의 제품 중 12개의 불량 제품이 발생한 경우, Chernoff Bound 를 바탕으로 12개 이상의 불량 제품이 관측될 확률의 upper bound를 구해보면 약 8.2%가 나온다 ($\delta = 2$).
1.4. Hoeffding’s Inequality
다음으로는 Hoeffding Inequality 에 대해 알아보자. Hoeffding Inequality는 $[l_i, u_i]$의 범위에 bounded 되어 있는 확률 변수 $X_i$ 들의 합 $X = \sum_{i=1}^N X_i$ 에 대해서 임의의 양수 $\theta>0$ 에 대해 다음의 probability bound를 제시한다. 확률변수들에 대한 분포 가정이 없다는 점에서 꽤나 실용적이라고 할 수 있다.
Hoeffiding inequality의 한가지 흥미로운 점은, tail bound가 모수 $\theta$ 에 대해 지수적으로 감소한다는 점이다. 이는 정규분포의 성질과 매우 유사한데, 사실 이는 중심극한 정리를 바탕으로 조금만 생각해보면 당연한 결과라는 것을 알 수 있다. 즉, 표본의 크기가 충분할 경우 중심극한 정리에 의해 확률변수의 합은 정규분포로 수렴한다는 점에서, 이를 바탕으로 asympotically exact한 바운더리를 구할 수 있기 때문이다.
여태까지 특정한 확률변수의 이론적 극단값을 제한시킬 수 있는 여러가지 수학적 부등식에 대해 살펴보았다. 이러한 부등식들은 그 가정 사항에 따라 probability bound의 strength가 달라진다는 점 역시 살펴보았는데, 이를 정리하면 다음과 같다.

Table 1: Comparison of different methods used to bound tail probabilities
1.5. The normal-based tail confidence tests
한편, 앞서 살펴본 부등식들과는 다르게, 만약 특정한 확률변수의 정확한 분포 (또는 근사 분포) 를 정의할 수 있다면 해당 분포에서의 누적확률밀도 값을 이용해서 tail bound를 정의할 수 있다. 이와 관련해서 현실속의 많은 문제들에서 우리는 중심극한정리에 의해 확률 변수의 근사적 분포를 정규분포로 설정할 수 있는 점은 꽤나 중요한 사실이다.
이러한 측면에서 교재에서는 구체적으로 정규분포와 t 분포에 대해서 소개하고 있는데, 크게 새로운 내용은 없으므로 대략적인 아이디어만 살펴보고 넘어가도록 하겠다. 이상치 탐지의 맥락에서 tail bound는 z-score $Z = \frac{X-\mu}{\sigma}$ 에 대한 표준 정규 분포에서의 누적 확률 밀도를 바탕으로 정의된다. 이처럼 서로 다른 $N$ 개의 샘플 별로 z-score 값이 정의되었다면, $V = \sum_{i=1}^N Z_i^2 \sim \chi^2(N)$ 의 성질을 이용해서 카이제곱분포를 바탕으로 유의 수준 $\alpha$ 아래에서의 confidence test를 정의할 수 있다 (e.g. 누적확률밀도가 0.95 이상이 되는 threshold를 이상치로 정의).
1.6. Visualization of extreme values with Box Plots
다소 ad-hoc한 방법이긴 하나, 전통적으로 통계학에서 이상치를 정의하는데 상자그림 (box plot) 이 많이 활용된다. 이는 통계학개론 등의 기초 통계학 수업에서도 단골로 등장하는 내용 중 하나인데, 상자 그림에서의 IQR (inter-quartile range) 값을 이용해서 이상치를 시각화 하고, tail bound를 정의할 수 있다. 흔히 사용되는 Tukey’s method는 $1.5 \times IQR$ 값을 이상치의 기준으로 설정한다. 크게 어려운 내용이 아니라 구체적으로 파고들 내용은 없지만, 한 가지 주목할만한 점은 만약 데이터의 분포가 정규 분포를 따르는 경우 Tukey’s method의 tail bound는 3-$\sigma$ method의 outlier threshold와 정확히 일치한다는 것이다. 또한 이러한 상자 그림은 이후 살펴볼 outlier ensemble 에서 모형의 성능을 시각화하는 목적으로도 자주 활용된다.
아래 그림은 각각 표준화된 균일 (uniform), 정규, 지수 분포를 따르는 데이터를 Tukey’s Box plot 기법으로 시각화한 것이다. 이 때 균일 분포에서는 이상치가 정의되지 않는 반면, 정규분포와 지수분포에서는 upper bound를 넘어가는 값들이 이상치로 정의된다. 또한 지수 분포의 경우 box 자체가 대칭이 아니라는 점도 주목할만 하다.

Figure 1: Visualizing univariate extreme values with box plots
2. Extreme-Value Analysis in Multivariate Data using boundary properties
다음으로는 한개 이상의 feature로 구성된 데이터에서 이상치를 정의하는 통계적 기법들에 대해서 살펴보자. 여기서 살펴볼 기법들은 다변량 데이터의 sample space에서 “boundary에 위치한 이상치들”을 잡아내는데 특히나 유용하다.

Figure 2: Example of multivariate extreme values
가령, 위와 같은 상황에서 데이터 포인트 $A$ 와 $B$ 를 살펴보자. 이 때 $A$ 는 세개의 클러스터의 안쪽에 위치한 반면, $B$ 는 클러스터들의 바깥쪽, 즉 boundary에 위치한 이상치라고 할 수 있다. 이러한 맥락에서 후술할 통계적 기법들을 이용하면 $B$ 와 같은 형태의 이상치를 효과적으로 판별할 수 있다. 단, 이와는 반대로 $A$ 는 발견하지 못할 가능성이 크다.
2.1. Depth-Based Outlier Detection Methods
해당 아이디어는 이상치들이 특정한 볼록 껍질 (i.e. convex hull) 의 가장 자리 (boundary) 에 있을 것이라는 가정을 바탕으로 한다. 사실 엄밀히 말하면 이는 통계적 접근이라기보다는 알고리즘적인 접근법이라고 할 수 있는데, 특정한 공간의 가장 자리에 위치한 값들을 아웃라이어로 파악한다는 점에서 이후 살펴볼 통계 방법론들과 아이디어가 비슷하기 때문에 간략히 살펴보고 넘어가도록 하겠다.
해당 알고리즘은 시각적으로 다음과 같이 나타낼 수 있다. 즉 데이터의 가장 바깥쪽에 위치한 데이터들을 순차적으로 제거하면서 레이어를 생성한다. 이러한 작업은 모든 데이터가 고려되었을 때까지 반복해서 수행되면, 이를 바탕으로 특정한 depth $k$ 까지의 레이어를 아웃라이어로 정의하게 된다.
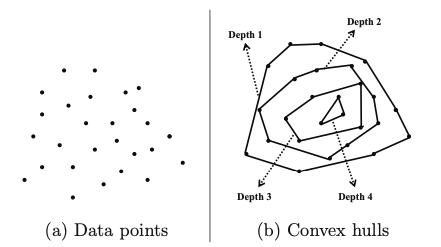
Figure 3: Depth-based outlier detection
해당 알고리즘에 대한 pseudo-code는 다음과 같다.

Pseudocode for finding depth-based outliers
한편, 이러한 접근법의 가장 큰 문제는 데이터의 크기와 차원수에 상당히 민감하다는 점이다. 따라서 데이터가 조금만 커져도 연산량이 너무 많아져 현실적으로 수행이 불가능해진다는 치명적인 단점이 있다. 이러한 점을 보완하기 위해 해당 알고리즘의 연산량을 줄일 수 있는 여러 기법들이 연구되었다 (참고1, 참고2).
2.2 Deviation-Based Outlier Detection Methods
위와 비슷한 맥락에서, 만약 특정한 공간의 가장 자리에 위치한 값들을 이상치로 정의할 수 있다면 해당 값들을 제거할 경우 데이터셋의 분산이 상당히 줄어들 것임을 직관적으로 생각해볼 수 있다. 이러한 관점에서 deviation-based method는 “smoothing factor” 라는 지표를 바탕으로 데이터셋의 분산을 가장 많이 감소시키는 데이터 포인트의 집합 $E$ 를 이상치로 정의한다.
구체적으로, 전체 데이터셋 $X$ 의 부분 집합 $R$ 에 대한 smoothing factor $SF(R)$ 은 다음과 같이 정의된다.
이 때, 이상치 탐지 과제는 모든 $R$ 에 대해 $SF(E) \geq SF(R)$ 를 만족시키는 데이터 집합 $E$ 를 찾는 것이다. 단, 이 과정에서 모든 데이터를 전부 고려할 경우 $2^N$ 만큼의 가능성이 존재하기 때문에 데이터의 개수가 조금만 커지면 연산량이 너무 많아진다는 한계점이 있다. 따라서 해당 논문에서는 효율적인 탐색을 수행하기 위한 BFS, random sampling 등의 기법이 제안되었다.
2.3 Angle-Based Outlier Detection Methods
Angle-based oullier detection method는 말 그대로 “각도”의 개념을 활용해서 가장 자리에 위치한 이상치들을 파악하려는 접근법이다. 아래의 그림을 살펴보자.
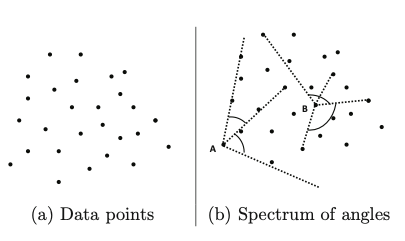
Figure 4: Angle-based outlier detection
직관적으로, 공간의 가장 자리에 위치한 데이터 포인트들은 해당 공간을 감싸고 있는 형태일 것이기 때문에, 내부에 위치한 다른 포인트들과 이루는 각도가 상대적으로 작을 것이라는 점을 생각해볼 수 있다. 이러한 측면에서 angle-based method 는 각 데이터 포인트가 다른 값들과 이루는 각도의 분산을 측정해서 그 값이 충분히 작은 것들을 이상치로 정의하게 된다.
좀 더 구체적으로 살펴보자면, 특정한 데이터 포인트 $X$ 가 서로 다른 두개의 점 $Y, Z$ 와 이루는 각도를 측정하기 위해 다음의 지표를 활용할 수 있다. 이 때 $<\cdot>$는 스칼라 곱을 의미하며, $||\cdot||$ 은 $L_2$-norm을 의미한다.
해당 지표는 간단히 말하자면 벡터 $(Y-X)$ 와 $(Z-X)$ 가 이루는 코사인 각도를 그 거리를 가중치로 삼아서 나눠준 것인데, 개념적으로 두 점이 멀리 위치하면 할 수록 지표의 값이 작아져 이상치로 판별될 가능성이 높아지게 된다. 이를 바탕으로 특정한 점 $X$에 대한 angle-based outlier factor $ABOF(X)$는 해당 지표의 분산으로 다음과 같이 정의된다.
한편, 이러한 접근법 역시 개별적인 데이터 포인트 전부를 각각 고려할 경우 복잡도가 $O(N^3)$ 로 연산량이 너무 과대해진다는 문제점이 있다. 따라서 $ABOF$ 를 좀 더 효율적으로 계산하기 위한 방안이 해당 연구에서 제안되었는데 관심이 있으면 읽어보기를 추천한다.
이 밖에도 해당 방법은 이상치 탐지 분야에서의 흔한 이슈인 차원의 저주 (curse of dimensionality) 를 피해갈 수 없다는 문제점 또한 있다. 많은 데이터셋의 경우, 차원이 증가함에 따라 데이터가 고차원 공간에서의 국소적 (local) 부분 공간에 밀집되어 분포하기 때문에 데이터 간의 거리가 점점 비슷해지는 (equidistant) 문제가 발생한다. 이 경우 앞서 살펴본 코사인 각도가 0.5로 수렴하게 된다.
2.4. The Mahalanobis Method (Distance Distribution-based Methods)
이상치 탐지에서 “distribution-dependent approach” 란 데이터를 특정한 통계 분포로 모델링하려는 시도이며, 이 과정에서 가장 많이 활용되는 것은 바로 다변량 정규분포이다. 이러한 맥락에서 다변량 정규분포를 간단히 복습해보자면, $d$ 차원의 공간에서 평균 벡터 $\mu_d$ 와 공분산행렬 $\Sigma_{d\times d}$ 을 갖는 다변량 정규분포를 따르는 확률 변수 $X$ 의 확률밀도함수는 다음과 같다.
이와 관련해서 mahalanobis distance 는 위 확률밀도함수의 exponent term과 관련이 있다. 구체적으로 이는 다음과 같이 정의된다.
자 그렇다면 mahalanobis distance의 의미를 이해해보자. 우선 이 역시 “distance”라고 불린다는 점에서, 특정한 공간에 위치한 두 점 사이의 거리를 측정하기 위한 개념이라고 파악할 수 있다. 그리고 위 정의를 바탕으로 할 때, 이는 어떠한 점 $X$ 와 특정한 데이터 클라우드(정규분포)의 중심점 (centroid) $\mu$ 사이의 거리를 측정하는 것이다. 이 과정에서 중간에 추가된 공분산행렬의 역행렬 $\Sigma^{-1}$ 은 모든 축(axis)의 상대적 크기를 고려해서 거리를 보정하는 역할을 수행하고 있다.
바로 이 부분에서 고차원 공간과 관련해서 상당히 중요한 개념이 하나 등장하는데, 이는 바로 “inter-attribute correlation” 이다. 직관적인 이해를 위해서 다음의 예시를 살펴보자.
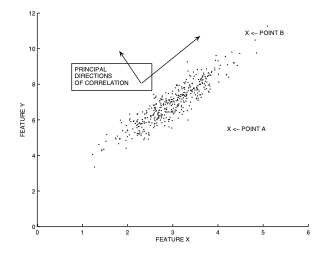
Figure 5: Extreme-value analysis in multivariate data with Mahalanobis distance
위 그림에서 데이터는 양의 상관계수를 갖는 2차원 다변량분포를 따른다고 할 수 있다.
이제 위 그림에서 두 점 $A$ 와 $B$ 가 각각 이상치인지 아닌지를 판단해보자. 데이터의 분포를 고려할 때, $B$ 보다는 $A$ 가 더 이상치에 가까울 것이라고 보는 것이 자연스러울 것이다. 이렇게 시각화를 할 수 있다면 한 눈에 바로 파악이 가능하나, 3차원을 넘어가는 공간에서 위처럼 시각적으로 이상치를 판단하는 것은 상당히 어려워진다는 한계점이 있다.
따라서 우리는 “거리”를 바탕으로 이상치를 정의해보도록 하겠다. 구체적으로, 위 데이터의 중심점은 대략적으로 $(3, 6)$ 정도로 보이는데, 해당 중심점과의 거리를 바탕으로 그 값이 크면 클 수록 이상치로 판단하는 것이 자연스러울 것이다.
이러한 맥락에서 가장 일반적인 유클리디안 거리를 사용해서 중심점에 대한 $A$와 $B$ 각각의 거리를 구한다고 해보자. 이 경우 우리의 의도와는 다르게, 중심점 $(3,6)$은 $B$ 보다 $A$ 와 더 가깝게 된다. 즉, 유클리디안 거리에서는 $A$ 보다 $B$ 가 더 이상치에 가까운 값이 되는 것이다. 이와 같은 문제점은 전체 공간에서 각 좌표축 간의 상대적 크기가 고려되지 않았기 때문에 발생한다. 즉 Figure 5에서 데이터는 양의 상관관계를 갖는 초평면을 따라 분포하기 때문에 X축과 Y축 각각에 대한 분산이 서로 다르다는 점에서 거리의 왜곡이 발생하는 것이다.
바로 이러한 문제점을 고려하기 위해 Mahalanobis distance는 특정한 점의 좌표들을 각 좌표축의 표준편차로 나눠준 다음 계산된 유클리디안 거리이다. 이 과정에서 공분산행렬은 바로 이러한 좌표축간의 상관관계를 함축적으로 요약한 통계량이라고 이해할 수 있으며, 따라서 Figure 5에서 중심점에 대한 Mahalanobis distance는 $B$ 에 비해 $A$ 가 더 멀어진다. 이처럼 “inter-attribute correlation” 이 자연스레 고려될 수 있다는 점은 Mahalanobis distance가 갖는 큰 장점이라고 할 수 있다. 실제로 많은 경우 Mahalanobis distance는 앙상블의 컴포넌트로 이상치 탐지 과제에서 활용된다.
한편, Mahalanobis distance를 계산하기 위해서는 공분산행렬의 역행렬을 구해야하기 때문에 차원수 $d$ 가 커질수록 역행렬 연산에 꽤나 큰 컴퓨팅 자원이 소모된다는 단점이 있다 (일반적으로 $O(n^3)$). 이러한 연산량을 줄이기 위해서, 공분산 행렬의 형태를 대각행렬로 제한하는 등의 아이디어가 활용될 수 있다. 반면, Mahalanobis distance는 데이터 사이즈 $n$ 에 대해서는 선형적인 연산 복잡도를 갖고 있다는 장점이 있다 ($O(n)$).
3. Probabilistic Mixture Models for Outlier Analysis
앞서 살펴본 Mahalanobis distance를 포함한 여러 기법들은 단 하나의 봉우리를 갖는 “unimodel dataset”에서는 좋은 성능을 발휘할지 몰라도, 여러개의 데이터 클러스터가 혼재된 “multimodal dataset”에 대해서는 그리 효과적이지 않을 수 있다. 가령 앞서 살펴본 Figure 2와 같은 예시에서는 서로 다른 세 개의 클러스터를 모델링 할 수 있어야만 $A$와 같은 점을 제대로 이상치로 분류할 수 있을 것이다.

Figure 2: Example of multivariate extreme values
이러한 맥락에서 “(statistical) mixture model” 이란, 특정한 형태를 갖는 “여러 개의” 분포를 데이터셋에 적합시키려는 아이디어이다. 가령 Figure 2에서는 서로 다른 평균 벡터와 공분산행렬을 갖는 정규분포 $G_1, G_2, G_3$ 를 바탕으로 mixture distribution을 정의할 수 있을 것이다. 구체적으로, 이는 mixture coefficient $\alpha$ 를 통해서 하나의 통합된 분포로 정의되는데, 직관적으로 $\alpha$ 는 각 분포에 속한 데이터의 비율 정도로 이해할 수 있다.
여기서 mixture coefficient와 각 분포의 모수는 데이터를 바탕으로 추정의 대상이 된다. 가장 일반적으로는 최대우도추정법 (maximum likelihood estimation) 이 사용되는데, 이는 주어진 데이터를 가장 잘 설명하는 모수를 찾으려는 것으로 이해할 수 있다. 계산의 편의를 위해 일반적으로는 로그를 취한 log-likelihood 값을 최대화 하는 모수 $\Theta$ 의 값들을 추정하게 되는데, 이를 수식적으로 나타내면 다음과 같다 (위 예시에서 $k=3$).
이 과정에서 우리는 1) 각 데이터 포인트가 어떠한 mixture component에서 나왔는지를 파악한 다음, 2) 각 mixture component에 속하는 데이터를 바탕으로 모수를 추정하는 과정을 반복하게 된다. 이러한 프레임워크는 자연스레 EM 알고리즘이 모수 추정에 활용될 수 있도록 한다.
- (E-step): 현 시점의 모수 $\Theta^{(t)}$ 를 바탕으로, 특정한 데이터 포인트 $X_i$ 에 대한 각 mixture component $G_r$ 에서의 사후 확률(posterior probability)을 도출한다.
- (M-step): E-step에서 구한 값을 바탕으로 $X_i$ 를 가장 높은 사후 확률을 갖는 $G_r$ 에 배정한 다음, 이를 바탕으로 각 $G_r$의 모수에 대한 MLE를 구한다.
이를 바탕으로 분포의 모수가 전부 추정되었다면, 이제 특정한 데이터 포인트에 대한 generative probability를 구체적인 값으로 도출할 수 있을 것이다. 이상치 탐지의 맥락에서 해당 likelihood 값은 직접적으로 outlier score가 되는데, 일반적으로는 로그를 취한 log-likelihood 값이 활용되며 해당 값이 낮을수록 이상치로 판별될 가능성이 커진다.
한편, 이와 같은 mixture model의 한가지 한계점은 바로 mixture component의 개수 $k$를 하이퍼파라미터로 직접 설정해줘야 한다는 점이다. 이상치 탐지에 대한 성능 역시 $k$에 크게 의존하는데, 가령 Figure 2에서 $k$ 를 3이 아닌 2로 설정할 경우 데이터를 제대로 설명하기가 어려울 것이다. 이처럼 실제로 대부분의 경우 구체적으로 $k$ 를 몇으로 설정할지에 대한 명확한 가이드라인이 없기 때문에, 해당 논문 등에서는 여러개의 $k$ 에 대한 앙상블을 적용하는 등의 방법을 제안하고 있다.
4. Limitations of probabilistic models for outlier analysis
일반적으로, 앞서 살펴본 Mixture model처럼 특정한 분포의 형태를 가정하는 parametric method는 다음과 같은 한계점을 갖고 있다.
- 데이터에 대한 분포 가정이 잘못된 경우 모형의 성능이 크게 떨어질 수 있다.
- 모수의 제약을 완화시킬수록 학습에 필요한 연산량이 증가하며, 이상치까지도 피팅시켜버리는 과대 적합 (overfitting) 문제가 발생한다 (e.g. 공분산 행렬의 제약이 없는 다변량 정규분포).
- 모수에 제약을 걸면 걸수록 데이터에 대한 과소 적합 (underfitting) 문제가 발생해 정상치(inlier)와 이상치(outlier)가 뚜렷하게 구분되지 않는다.
위와 같은 문제점을 해결하기 위해 일반적인 분류 문제에서는 훈련용 데이터로 모형의 모수를 추정한 다음, 평가용 데이터를 바탕으로 모형의 성능을 평가하는 것을 통해 최적의 모수를 찾게된다. 하지만 이러한 접근법은 당연하게도 이상치에 대한 라벨값이 부재한 이상치 탐지 과제에서는 수행될 수 없다. 따라서 이상치 탐지와 같이 비지도 학습으로 수행되는 과제에서는 모형에 사용된 분포의 형태에 대한 가정과 모수의 제약조건에 대한 가정 등을 객관적으로 평가하기가 어려워지는 것이다.
이와 같은 tradeoff는 단순히 통계 모형 뿐만 아니라 이후 살펴볼 (거의 모든) 이상치 탐지 알고리즘에도 동일하게 적용되는 문제점이기 때문에, 효과적인 이상치 탐지 모형은 학습 과정에서 일정한 규제(regularization)를 통해서 과대 적합과 과소 적합의 밸런스를 잘 맞추는 것이 중요하다.
Reference
- Aggarwal, C. C. (2013). Outlier Analysis. Springer. ISBN: 978-1-4614-6396-2
- T. Johnson, I. Kwok, and R. Ng. Fast Computation of 2-dimensional Depth Contours. ACM KDD Conference, 1998.
- I. Ruts and P. Rousseeuw. Computing Depth Contours of Bivariate Point Clouds. Computational Statistics and Data Analysis, 23, pp. 153–168, 1996.
- A. Arning, R. Agrawal, and P. Raghavan. A Linear Method for Deviation Detection in Large Databases. ACM KDD Conference, 1996.
- H.-P. Kriegel, M. Schubert, and A. Zimek. Angle-based Outlier Detection in High- Dimensional Data. ACM KDD Conference, 2008.
- A. Emmott, S. Das, T. Dietterich, A. Fern, and W. Wong. Systematic Construction of Anomaly Detection Benchmarks from Real Data. arXiv:1503.01158, 2015.