[Outlier Analysis] High-dimensional Outlier Detection
대부분의 현실적인 이상치 탐지 시나리오에서 우리는 고차원의 데이터셋을 다루게 된다. 많게는 수백, 수천개의 차원을 갖고 있는 데이터에서 앞서 살펴본 다양한 이상치 탐지 기법들은 제대로 작동하지 않을 우려가 커지는데, 이는 소위 말하는 차원의 저주 (curse of dimensionality) 에 의해 데이터가 고차원 공간의 매우 국소적인 부분 공간에 밀집해서 분포하기 때문이다. 이를 “data sparsity” 또는 “distance concentration” 이라고 일컫는다. 가령, 이상치 탐지에 흔히 활용되는 LOF 등의 거리 기반 알고리즘을 생각해보자. 해당 방법론들에서 아웃라이어는 다른 데이터들에 비해 상대적으로 “멀리 떨어진” 값들로 정의되지만 고차원 공간에서 이와 같은 거리에 대한 척도는 아웃라이어에 대한 지표로서의 기능을 제대로 수행하지 못하게 된다.
따라서 고차원 공간에서의 성공적인 이상치 탐지를 위해서는 데이터가 실제로 분포하고 있는 국소적인 부분 공간 (locally-relavant subspace) 을 잡아내는 것이 필수적이다. 하지만 이는 결코 만만한 작업이 아닌데, 그 이유는 수 많은 차원 중에서 어떤 차원들이 데이터를 잘 설명하는지를 사전에 알 수가 없으며, 모든 차원들에 대한 조합을 일일히 고려하는 것이 불가능하기 때문이다. 가령, 10차원 정도만 되더라도 가능한 차원의 모든 조합은 $2^{10} = 1024$ 로 상당한 컴퓨팅 자원을 소모할 것이다. 이와 더불어 이상치 탐지를 위해서는 정상적인 데이터와 아웃라이어 간의 상대적 위치를 최대한 극대화 또는 보존시키면서 저차원의 공간을 탐색해야 한다는 점에서 주성분 분석 (PCA) 등의 보편적인 차원축소 방법론 역시 쉽게 활용할 수 없게 된다.
해당 내용을 직관적으로 이해하기 위해 다음의 예시를 살펴보자. 이는 (가상의) 고차원 데이터셋에서 랜덤하게 선택된 두개의 축에 데이터를 투영 (projection) 시킨 것이다.
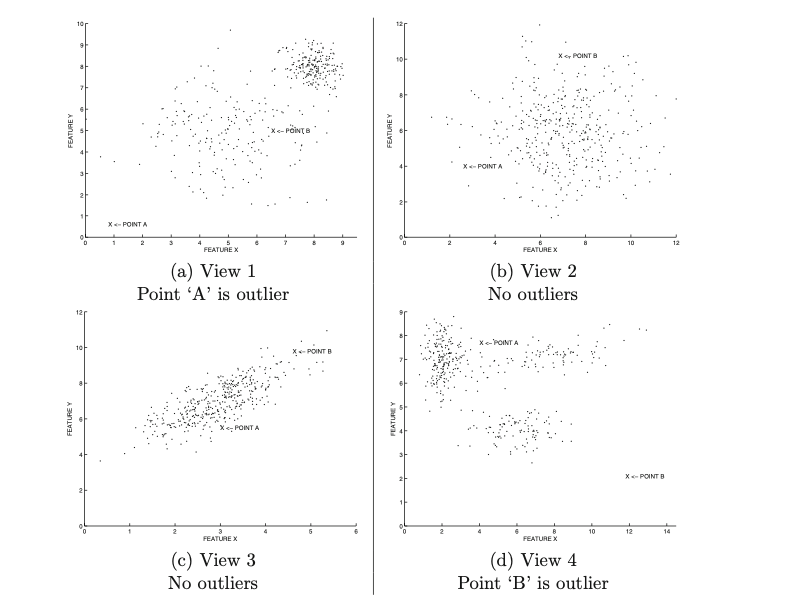
Figure 1: The outlier behavior is masked by the irrelevant attributes in high dimensions.
위 데이터에서 $A$ 와 $B$ 는 실제로 다른 generative process로 부터 생성된 아웃라이어이다. 이와 관련해서 그림 (a) ~ (d) 는 모두 동일하게 2차원의 부분 공간임에도 불구하고 그 시각에 따라서 $A$, $B$ 가 아웃라이어로서 부각이 될 수도, 되지 않을 수도 있다는 점을 보여준다. 가령, (b)와 (c)는 이상치 탐지의 맥락에서 전혀 유용하지 않은 부분 공간이라고 할 수 있다.
이처럼 아웃라이어는 전체 데이터셋의 아주 일부분의 차원에서만 발견할 수 있는 경우가 많다. 예를 들어, 어떠한 생산 공정에서 만들어진 제품이 수백개의 성능 점검 테스트를 거친다고 가정해보자. 이 과정에서 앞선 수백개의 테스트를 통과했다 하더라도, 마지막 단 한개의 테스트를 통과하지 못할 경우 해당 제품은 이상치로 분류되어 폐기될 것이다. 이러한 맥락에서 해당 포스트에서 살펴볼 subspace outlier detection은 (일반적으로) 차원이 늘어남에 따라 정보량이 비례해서 증가하지만은 않는다는 가정을 바탕으로 한다. 오히려 불필요한 차원 (irrelavant feature)들은 아웃라이어들의 존재를 숨기는 “masking effect”를 초래할 가능성이 있다.
이와 관련해서 이상치 탐지를 위한 부분 공간을 정의하는데 활용될 수 있는 여러가지 아이디어들을 살펴보도록 하자.
1. Axis-parallel Subspaces
1.1. Subspace Outlier Detection
“Axis-parallel subspace”란 전체 데이터셋의 차원 (feature) 에 대한 부분 집합을 의미한다. 가령, 총 6개의 feature $X_1,\dots, X_6$ 를 갖고 있는 데이터를 ${X_1, X_2}$ 의 단 두개의 차원으로 투영할 경우, $\text{Span}({X_1, X_2})$ 가 바로 axis-parallel subspace라고 할 수 있다. 이는 아웃라이어들이 특정한 몇개의 차원에 의한 부분 공간에서 더욱 극명하게 보여질 수 있다는 아이디어를 바탕으로 하는데, 실제 상황에서는 여러개의 부분 공간을 임의로 선정한 다음, 해당 공간들에서의 이상치 탐지 결과를 수합해서 최종적으로 아웃라이어를 판단하는 앙상블 기법이 주로 활용된다. 이후 살펴볼 feature bagging, rotated bagging, isolation forest 등이 그 대표적인 예시라고 할 수 있다.
이처럼 전체 데이터셋의 부분 공간에서 아웃라이어를 파악하려는 시도를 “subspace outlier detection” 이라고 일컫는다. 이는 해당 논문에서 처음으로 제안되었는데, 저자들은 데이터의 부분 공간 중 비정상적으로 낮은 밀도 (density) 를 갖는 저차원의 공간들을 유전학적인 알고리즘을 바탕으로 탐색한 다음, 데이터들이 해당 부분 공간에 포함되는지 여부를 바탕으로 아웃라이어를 정의하려는 접근법을 제안했다. 즉, 해당 방법론의 핵심은 바로 낮은 밀집도를 갖는 저차원 공간을 모델링하는 것이라고 할 수 있으며 이 과정에서 컴퓨팅 속도가 주된 이슈가 된다. 이와 관련해서 탐색의 효율성을 높일 수 있는 다양한 방법론들이 후속 연구들에 의해 제안되었다 (참고1, 참고2).
1.2. Feature Bagging
한편, 위 방법과는 대조적으로 부분 공간에 대한 탐색 자체가 완벽히 랜덤하게 수행될 수도 있다. 이러한 기법을 바로 “feature bagging” 또는 “random subspace ensemble” 방법이라고 부르는데, 대략적인 개요는 다음과 같다:
- 데이터셋의 차원 수 $d$ 에 대해, $d/2$ 에서 $d-1$ 사이의 랜덤한 정수 (integer) $r$ 을 선택한다.
- 데이터셋에서 랜덤하게 $r$ 개의 feature를 비복원추출하여 차원 축소된 데이터셋 $D_r$ 을 얻는다.
- $D_r$ 에 대해 이상치 탐지 모형 $O$ 를 적용한다.
- 1 - 3 의 과정을 앙상블의 개수 $t$ 만큼 반복한 다음 결과를 수합해서 아웃라이어를 정의한다.
해당 방법은 다소 나이브한 것처럼 보일 수 있으나, 실제 적용시 많은 상황에서 full-dimensional approach에 비해 우월한 성능을 보일 수 있다는 점이 연구된 바 있다 (참고). 비록 부분 공간에 대한 탐색이 optimal하게 이루어지지는 않으나, 여러개의 부분 공간의 결과를 수합해서 정의된 아웃라이어는 충분히 많은 부분 공간들에서 아웃라이어임이 드러난, 이른바 “강건한 아웃라이어 (robust outliers)” 라는 특징이 있다. 이처럼 여러개의 모형을 개별적으로 학습시켜 (weak-learners) 더 나은 결과를 얻을 수 있다는 점은 classification 도메인의 선행 연구를 통해 이론적으로 증명된 부분이다.
1.3. Projected Clustering Ensembles
군집 분석에서 “projected clustering methods” 란 각각의 데이터 포인트를 저차원의 공간에 위치하는 클러스터에 할당하는 방법론이다.

Figure 2: Example 2D space with subspace clusters
위 그림을 통해서 확인할 수 있듯이, 일정한 거리에 대한 척도를 바탕으로 데이터들은 저차원의 공간에 투영된다. 이 과정에서 정상적인 데이터들이 속한 클러스터에는 비슷한 성질을 갖는 데이터 포인트들이 분포할 것이며, 아웃라이어들에 대한 클러스터에는 상대적으로 성질이 균등하지 않은 데이터 포인트들이 많이 포함될 것이다. 이러한 맥락에서 최종적인 아웃라이어는 각 클러스터에 속한 데이터 포인트들의 상대적 크기, 차원수, 중심점까지의 거리 등을 고려해서 판단되며, 일반적으로 여러개의 차원에 대한 결과를 앙상블하여 결과를 도출하는 방식이 사용된다. 대표적으로는 PROCLUS 클러스터링 알고리즘을 바탕으로 하는 OutRank 가 있다.
1.4. Isolation Forests
Isolation forest는 classification 도메인에서 저명한 random forest 기법을 비지도 학습에 맞게 변형한 알고리즘이라고 할 수 있다. Isolation forest의 핵심 아이디어는 데이터를 랜덤하게 선택된 axis-parallel subspace로 반복해서 분할해나가며 각각의 데이터 포인트를 특정한 leaf (노드) 에 고립시키는 방식으로 트리 모형을 학습시키는 것이다. 이 과정에서 아웃라이어들은 표본 공간에서 상대적으로 희소한 부분 공간에 위치할 것이기 때문에, 학습의 초기 단계에서 특정한 leaf로 분류될 가능성이 높아진다. 이러한 맥락에서 outlier score는 각 데이터 포인트가 위치한 leaf와 root까지의 거리로 정의되며, 그 값이 작을수록 아웃라이어일 가능성이 높아진다 (이미지 출처).

Figure 3: Example of Isolation Forest
이와 같이 여러개의 병렬적인 “isolation tree” 를 하나로 합친 것이 바로 “isolation forest”이다. 따라서 자연스럽게 이는 앙상블 기법을 활용한 subspace outlier detection 방법론이라고 할 수 있으며, 이 때 각각의 가지 (branch)는 하나의 지역적인 부분 공간 (local subspace)에 대응된다.
한편, 다른 subspace outlier detection 방법론들에 비해 Isolation forest는 컴퓨팅 속도의 측면에서 상당한 장점을 갖는다. 논문의 저자들은 각 트리의 훈련 과정에서 전체 데이터셋의 일부분을 샘플링해서 학습을 진행하는 것을 제안했는데, 이로 인해 모델 학습에 대한 시간 복잡도가 일정한 상수로 고정되어 큰 효율성을 갖는다는 특징이 있다. 이 밖에도 학습 시간의 효율을 높이기 위해 첨도 (kurtosis)를 활용하여 트리 분할에 사용될 feature를 선정하는 것과, 트리를 끝까지 분할시키지 않고 일정한 기준을 넘어가면 조기 종료시키는 아이디어가 저자들에 의해 제안되었다. 이러한 특징들에 의해 isolation tree는 앙상블 학습을 이론적인 기반으로 하는 “extremely randomized algorithm” 이라고 할 수 있다.
1.5. Selecting High-Contrast Subspaces (HiCS)
앞서 살펴본 feature bagging의 경우, 비록 subspace에 대한 탐색이 랜덤하게 이루어지더라도 여러개의 subspace에 대한 결과를 하나로 종합하는 과정에서 더 robust한 결과를 얻을 수 있을 것이라는 앙상블 학습의 아이디어를 바탕으로 이루어졌다. 이러한 아이디어 자체는 물론 타당하나, 차원이 감소하는 과정에서 일정량의 정보 손실 (information loss)이 발생할 수 밖에 없다는 점은 연구자들로 하여금 어떻게 하면 이상치에 대한 정보량을 최대로 보존하는 “최적의” 부분 공간을 찾을 수 있을지에 대한 논의를 불러일으키는 계기가 되었다.
이러한 맥락에서 제안된 HiCS 방법론은 통계적 가설 검정을 통해서 이상치들이 더 “잘” 드러나는 high-contrast subspace를 선택하려는 시도이다. 즉 feature bagging과는 다르게 subspace에 대한 탐색이 일정한 기준을 갖고 optimal하게 이루어진다는 점이 그 핵심이라고 할 수 있다. HiCS 알고리즘의 대략적인 개요는 다음과 같다:
-
Apriori algorithm을 바탕으로 high-contrast subspace를 정의한다.
- 해당 탐색은 high-contrast subspace의 경우 데이터의 분포가 상당히 non-uniform할 것이라는 가정을 바탕으로 한다.
- 이를 판단하기 위해, 선택된 $p$ 차원의 subspace에서 $\alpha$의 너비를 갖는 랜덤한 rectangular region을 정의한다. ($\alpha < 1$)
- 전체 데이터의 개수가 $N$ 이라고 했을 때, 만약 데이터의 분포가 uniform 할 경우 해당 rectangular region의 각 축에는 대략적으로 $N\cdot \alpha^{1/p}$ 개의 데이터가 포함되었을 것이다 (rectangular region 전체에는 $N \cdot \alpha$ 개)
- 이에 대한 통계적 가설 검정을 진행한다. 만약 uniform이라는 가정 아래의 이론적인 데이터 분포와 실제 데이터의 분포 간에 차이가 많이 날 경우, 해당 subspace는 high-contrast subspace라고 판단된다.
-
정의된 high-contrast subspace에 대해 이상치 탐지 알고리즘을 적용한 다음 결과를 도출한다.
- 논문에서는 LOF가 사용되었다.
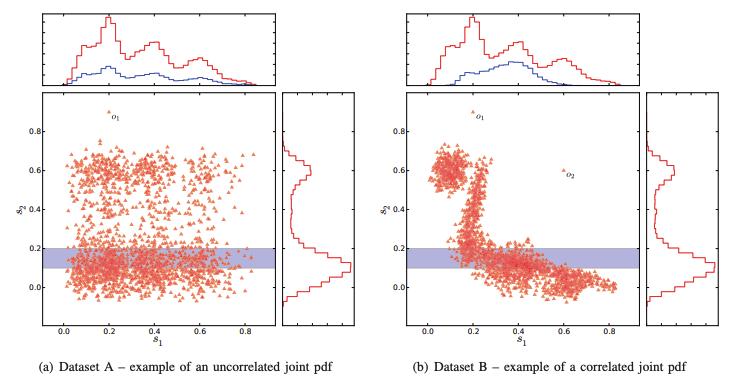
Figure 4: high vs. low contrast (출처: original paper)
해당 내용을 좀 더 직관적으로 이해하기 위해 Figure 4의 예시를 살펴보자. 왼쪽의 그림처럼 두 feature (x, y 축) 간의 상관관계가 낮은 subspace의 경우, 특정한 rectangular region에 포함된 데이터의 분포 역시 상대적으로 uniform한 것을 확인할 수 있다 (그래프 위쪽의 파란색 히스토그램). 반면, 오른쪽과 같은 high-contrast subspace의 경우는 rectangular region에서의 데이터의 분포가 uniform하지 않으며, 우리가 찾고자 하는 이상치 역시 상대적으로 더욱 부각되는 효과를 갖고 있다. 따라서 HiCS는 주어진 데이터로부터 오른쪽과 같은 부분 공간을 뽑아내는 것이 그 목표라고 할 수 있다.
한편, 해당 방법의 한가지 단점은 부분 공간을 정의하는 과정에서 꽤나 많은 컴퓨팅 자원을 소모한다는 점이다. 특히나 부분 공간별로 샘플 (rectangular region)을 정의한 다음 이를 바탕으로 통계적 가설 검정을 수행하는 apiori algorithm은 데이터셋의 크기에 민감할 수 있다. 이에 대한 한가지 해결 방안은 high-contrast subspace에 대한 지표로 가설 검정이 아닌 첨도 (kurtosis) 등의 보다 간단한 지표를 활용하는 것이다. 혹은 실시간적인 이상치 탐지가 필요한 도메인의 경우 (e.g. streaming data), 앞서 살펴본 feature bagging 등의 기법을 활용하는 것이 오히려 효과적일 수도 있다.
1.6. Local Selection of Subspace Projections
앞서 살펴본 방법들과 다르게, 해당 논문에서 제안된 OUTRES 라는 방법론은 이상치 탐지를 위한 최적의 subspace을 각 데이터 포인트의 관점에서 정의한다.
대략적으로, 해당 방법론에서는 각 데이터 포인트 $X^{(*)}$ 마다 “relevant” 한 subspace \(S^{(*)} = \{S_1, \dots, S_k \}\) 를 정의한 다음, 개별적인 subspace $S_i$에서의 outlier score $O(S_i, X^{(*)})$ 를 전부 곱한 값 $OS(X^{(*)}) = \prod_{i=1}^k O(S_i, X^{(*)})$ 이 충분히 작은 엔트리들을 아웃라이어로 정의하게 된다. 이 과정에서 “relevant subspace” 를 판단하는 기준으로는 통계적 가설 검정이 활용되는데, HiCS에서 살펴본 것과 유사하게 특정한 subspace에서의 데이터의 분포가 uniform하다는 가정 아래에서의 분포와 실제 데이터의 분포를 비교하려는 아이디어를 바탕으로 한다.
즉, 아래의 그림에서처럼 데이터의 분포가 상대적으로 uniform한 “scattered subspace” 를 통계적 가설 검정을 통해 일차적으로 필터링한 다음, 해당 가설 검정을 통과한 (dense) subspace에서 $X^{(*)}$ 가 주변 값들에 비해 충분히 차이가 나는 경우에 대해서만 outlier score를 계산하는 것이다. 이를 통해 각 데이터 포인트는 자기 자신을 가장 잘 설명할 수 있는 subspace에서 이상치인지에 대한 여부를 평가받게 된다.

Figure 5: Relevant subspace projections (출처: original paper)
이러한 접근법은 선택되는 subspace가 각 데이터 포인트에 최적화되어 있다는 점에서 학습 과정에 사용된 데이터에서는 좋은 성능을 발휘할 수 있으나, 이후 새로운 데이터에 대해서는 그만큼의 성능을 발휘하지 못할 가능성이 높다는 점이 한 가지 우려 사항이다. 또한 학습 과정에서 모든 데이터에 대해서 relevant한 subspace를 일일히 정의하기 때문에 속도적인 측면에서도 이슈가 발생할 수 있을 것이다.
2. Generalized Subspaces
앞서 살펴본 “axis-parallel” 한 subspace 들은 많은 경우 효과적으로 이상치를 잡아낼 수 있지만, 만약 데이터가 저차원 공간에서 임의의 군집 (매니폴드)의 형태로 분포할 경우에는 제대로 작동하지 않을 수 있다. 이게 무슨 말인지를 다음의 예시를 통해서 살펴보자.
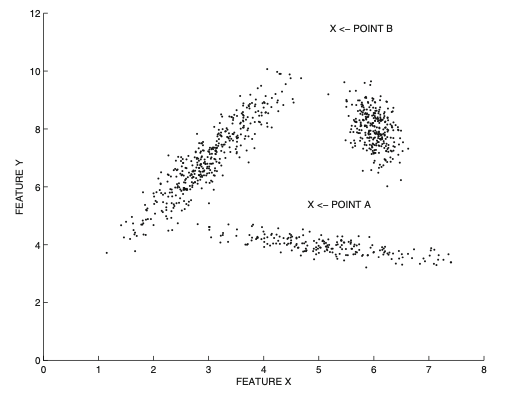
Figure 6: Example of arbitrarily oriented data along different directions of correlation
위와 같은 형태의 데이터를 앞서 살펴본 방법들처럼 특정한 축 (feature)에 투영한다고 해보자 (axis-parallel). 이 경우, 어떤 축을 선택하더라도 포인트 $A$ 는 이상치로 분류되지 않을 것이다. 또한 위 데이터의 경우 전체적인 맥락에서의 상관 관계, 즉 “global direction” 이 존재하지 않기 때문에 PCA와 같은 차원축소 기법 역시 활용될 수가 없다.
이러한 문제점을 해결하기 위해, 이상치 탐지 분야에서는 임의의 축을 기준으로 데이터를 투영시키는, 이른바 “generalized subspace analysis” 라는 리서치 토픽이 존재한다. 이렇게 될 경우 고려 가능한 projection axis의 개수가 무한하게 증가하기 때문에 단 하나의 optimal한 subspace를 찾는 것은 더 이상 불가능해진다는 단점이 있는데, 비록 optimal 하지는 않더라도 앙상블 학습을 통해서 기존 방법론들에 비해 훨씬 좋은 성능을 보일 수 있다는 점이 여러 연구들에서 경험적으로 입증된 바 있다. 특히나 앞선 방법들에서는 파악할 수 없었던 저차원의 매니폴드에 데이터가 국소적으로 분포되어 있는 형태의 데이터셋에서 이상치를 탐지할 수 있다는 상당한 장점을 갖고 있다.
단, 모든 문제가 그렇듯이 공짜 점심은 없다. 앞선 axis-parallel subspace에 비해 일반적인 subspace를 ad-hoc하게 찾는 과정은 그 이상의 컴퓨팅 자원을 소모하며, 최적화의 관점에서 고차원 공간에서의 optimal subspace를 찾는 것은 현실적으로 불가능하다. 따라서 우리는 필연적으로 앙상블 학습에 의존할 수 밖에 없는데, 이러한 맥락에서 해당 섹션에서는 이른바 “Rotated Bagging” 이라고 불리는 subspace sampling 방법에 대해서 살펴보려고 한다.
2.1. Rotated Subspace Sampling
“Rotated subspace sampling”, 또는 “rotated bagging” 은 앞서 살펴본 feature bagging을 일반적인 부분 공간으로 확장시킨 개념이라고 볼 수 있다. 즉, feature bagging에서는 여러개의 축 (feature) 중에서 임의로 몇개를 선택하는 방식으로 차원 축소가 이뤄졌다면, rotated bagging은 랜덤한 회전 축 (rotation axis)을 정의한 다음 이를 바탕으로 데이터를 저차원의 부분 공간으로 투영시키게 된다. 해당 논문에서 제안된 rotated bagging의 적용 절차는 다음과 같다:
-
Random rotation axis를 정의한다.
-
데이터셋의 차원 수를 $d$, 부분 공간의 차원 수를 $r$ 이라고 할 때, 모든 축에 대해 $[-1, 1]$ 의 범위에서 정의되는 다변량 균일분포 (multivariate uniform distribution)로 부터 $d \times r$ 크기의 랜덤 행렬 $R$ 을 샘플링한다. 해당 논문에서는 $r=\lceil 2+\sqrt{d}/2 \rceil$ 을 기본값으로 제안했다.
-
$R$ 의 각 열에 대해 그람-슈미트 직교화 (Gram-Schmidth orthogonalization)를 적용한다. 이로 인해 생성되는 행렬 $R^*$ 의 각 열이 바로 rotated subspace의 기저 (basis)가 된다.
-
-
앞서 정의한 rotation axis를 통해 데이터셋을 부분 공간으로 투영시킨다.
- 원래의 데이터셋을 $D$ 라고 할 때, 투영된 데이터는 $N \times r$ 크기의 $D^* = D R^*$ 이다.
-
$D^*$ 에 대해서 이상치 탐지 알고리즘을 적용한다.
-
1 ~ 3의 과정을 앙상블 개수만큼 반복한 다음, 결과를 수합해서 최종적으로 이상치를 정의한다.
이처럼 rotated bagging을 사용할 경우, 각 앙상블 컴포넌트에 대한 부분 공간들은 서로 다른 이상치들을 모델링하게 된다. 그리고 이러한 결과를 하나로 합치는 과정을 통해 보다 robust한 결과를 얻을 수 있는 것이다. 아래의 그림은 가상의 3차원 데이터에 서로 다른 두개의 회전 축을 기반으로 데이터를 투영시킨 결과인데, 이를 통해 subspace 마다 드러나는 이상치들이 서로 다른 것을 확인할 수 있다.

Figure 7: Examples of rotated projection
이처럼 여러 weak-learner 들의 결과를 조합하는 것을 통해 representational bias를 줄일 수 있다는 사실은 앙상블 학습의 큰 장점이다.
Reference
- Aggarwal, C. C. (2013). Outlier Analysis. Springer. ISBN: 978-1-4614-6396-2
- C. C. Aggarwal and P. S. Yu. Outlier Detection in High Dimensional Data. ACM SIGMOD Conference, 2001.
- J. Zhang, Q. Gao, and H. Wang. A Novel Method for Detecting Outlying Subspaces in High-dimensional Databases Using Genetic Algorithm. ICDM Conference, 2006
- J. Zhang and H. Wang. Detecting Outlying Subspaces for High-Dimensional Data: the New Task, Algorithms and Performance. Knowledge and Information Systems, 10(3), pp. 333–355, 2006.
- A. Lazarevic and V. Kumar. Feature Bagging for Outlier Detection. ACM KDD Con- ference, 2005
- T. Dietterich. Ensemble Methods in Machine Learning. First International Workshop on Multiple Classifier Systems, 2000.
- C. C. Aggarwal, C. Procopiuc, J. Wolf, P. Yu, and J. Park. Fast Algorithms for Pro- jected Clustering. ACM SIGMOD Conference, 1999.
- E. Muller, I. Assent, P. Iglesias, Y. Mulle, and K. Bohm. Outlier Analysis via Subspace Analysis in Multiple Views of the Data. ICDM Conference, 2012.
- F. T. Liu, K. M. Ting, and Z.-H. Zhou. Isolation Forest. ICDM Conference, 2008.
- F. Keller, E. Muller, K. Bohm. HiCS: High-Contrast Subspaces for Density-based Outlier Ranking. IEEE ICDE Conference, 2012.
- E. Muller, M. Schiffer, and T. Seidl. Statistical Selection of Relevant Subspace Pro- jections for Outlier Ranking. ICDE Conference, pp, 434–445, 2011.
- C. C. Aggarwal and S. Sathe. Theoretical Foundations and Algorithms for Outlier Ensembles. ACM SIGKDD Explorations, 17(1), June 2015.