[Outlier Analysis] Outlier Ensembles

2022, Aug 09

데이터 마이닝에서 앙상블 기법은 다양한 알고리즘들의 성능을 향상시키기 위해 활용될 수 있는 간단하면서도 효과적인 방법이다. 앙상블 기법의 핵심적인 아이디어는 서로 다른 알고리즘 (base detector)의 결과를 하나로 합쳐서 최종적인 결과를 도출하려는 것인데, 이는 각 알고리즘마다 데이터셋에서 “특화된” 부분이 있다는 전제를 바탕으로 약한 학습기 (weak-learners) 여러개의 결과를 통해 더 나은 결론에 다다를 수 있다는 이른바 “대중의 지혜 (the wisdom of crowds)“를 그 기반으로 한다. 이러한 앙상블 기법은 클러스터링, 분류, 이상치 탐지, 추천 시스템 등 데이터 마이닝의 다양한 분야 및 시계열, 네트워크, 평점 데이터 등 광범위한 데이터 도메인에서 성공적으로 활용되고 있다.

한편, 그 유용성에도 불구하고 앙상블 기법이 이상치 탐지에 활용되기 시작한 것은 다른 분야에 비해 상대적으로 그 역사가 길지 않다. 앙상블 기법이 가장 효과적으로 사용되는 분류 (classification) 도메인과 비교했을 때, 이에 대한 단편적인 이유는 바로 “라벨값의 부재” 때문이라고 할 수 있다. 가령, 주어진 라벨값을 학습에 활용하는 부스팅 등의 supervised ensemble algorithm과는 다르게, 이상치 탐지를 위해 개발된 모형들은 그 특성상 라벨, 즉 response가 없다는 가정 아래에서 (fully) unsupervised learning을 수행한다. 이처럼 이상치에 대한 ground-truth를 알 수 없는 환경에서는 앙상블 학습의 장점이라고 할 수 있는 특정한 알고리즘의 부족한 부분을 다른 알고리즘을 통해 집중적으로 학습시켜 보완하는 학습 전략이 사용될 수 없다는 문제점이 있다.

하지만 이러한 태생적인 한계점에도 불구하고, 이상치 탐지에 앙상블 기법을 적용하는 것은 분명한 장점이 있다. 그 대표적인 사례는 바로 이전 포스트에서 살펴보았던 “subspace outlier detection” 인데, 특정한 아웃라이어의 탐지에 특화된 부분 공간 여러개의 결과를 하나로 합치는 것을 통해 좀 더 강건한 (robust) 결과를 얻을 수 있다는 점은 여러 선행 연구들에서 경험적으로 입증된 사실이다. 이러한 맥락에서 unsupervised task에서도 각 알고리즘들의 “불확실성”을 줄이기 위한 목적으로 앙상블이 활용될 수 있다. 이와 관련해서 해당 포스트에서는 이상치 탐지에서 앙상블 기법이 어떻게 활용될 수 있을지에 대한 개괄적인 내용을 간단히 살펴보려고 한다.

Categorization of Ensemble Methods
Design of Ensemble Methods
Theoretical Foundations of Outlier Ensembles
Variance-reduction ensembles
Bias-reduction ensembles

1. Categorization of Ensemble Methods

우선 첫 번째로, 앙상블 기법은 어느 부분에서 앙상블이 발생하는지에 따라서 크게 다음의 두가지의 카테고리로 분류될 수 있다.

Model-centric ensembles
- 해당 앙상블은 이상치 탐지에 활용되는 모형의 관점에서 다양성이 발생한다.
- e.g. 서로 다른 독립적인 모형의 결과를 앙상블, 특정한 모형의 여러 하이퍼파라미터에 대한 결과를 앙상블
Data-centric ensembles
- 해당 앙상블은 모형의 인풋값, 즉 데이터의 관점에서 다양성이 발생한다.
- 간단히 말하자면 주어진 데이터를 여러 형태로 변형해서 각각에 대해 모형을 학습시키는 것이다.
- e.g. data subsampling, feature bagging, random projections, noise addition, …

이와 비슷하지만 약간 다른 맥락에서, 앙상블에 사용되는 base detector 간의 관계성에 따라 다음의 두 카테고리로 앙상블 기법을 분류하기도 한다.

Independent ensembles
- 해당 앙상블에서 base detector들의 학습은 완벽히 독립적으로 수행된다. 즉, 이전 모형의 학습 결과가 이후 모형의 학습에 영향을 미치지 않는다.
- 이상치 탐지와 관련한 대부분의 앙상블 알고리즘들이 해당 카테고리에 속한다고 할 수 있다.
Sequential ensembles
- 특정한 base detector가 학습되는 과정에서 이전 단계의 결과를 참고해서, 더 나은 결과를 유도한다.
- 이것의 대표적인 사례는 분류 도메인의 부스팅 기법이라고 할 수 있다.
- 이상치 탐지에서는 비록 그 사례가 적으나, 이전 단계에서 “이상치”로 판별된 데이터들을 이후 단계의 학습에서 제외시키는 것을 통해 “normal”인 데이터만으로 구축된 모형을 만드는 “OOD (out-of-distribution) Detection” 등이 있다.

단, 이러한 구분은 서로 배타적이 아니며 방법론의 성격에 따라 “Independent ensemble” 모형이 “model-centric”과 “data-centric” 두가지 전부에 속할 수도 있다 (e.g. Isolation Forest). 이는 단지 이상치 탐지와 관련해서 앙상블 학습이 어떤 관점에서 수행될 수 있을지와 이에 따른 특징이 어떻게 구분되는지를 대략적으로 파악하기 위함인데, 이러한 구분에 대한 좀 더 디테일한 논의는 해당 텍스트북의 p.188을 참고하자.

2. Design of Ensemble Methods

다음으로는 앙상블 방법의 디자인, 즉 서로 다른 base detector의 결과를 어떤 방법으로 수합할지에 대해서 논의를 이어가보자.

2.1. Score Normalization

노테이션의 편의상, $N \times d$ 크기의 데이터셋 $D$ 를 바탕으로 학습된 $m$ 번째 base detector $B_m$에 대해, $i$ 번째 데이터 포인트 $D_{(i)}$에 대해서 얻어진 outlier score를 $s_m(i)$ 라고 정의하자. 즉, 모든 $D_{(i)}, \; (i=1,\dots, N)$ 에 대해서 $B_1, \dots, B_m$ 을 바탕으로 $s_1(i), \dots, s_m(i)$ 의 총 $m$ 개의 outlier score가 얻어지는 것이며, 이로부터 하나의 outlier score $S(i)$ 가 앙상블의 결과로 정의된다.

한편, 이 과정에서 만약 각각의 base detector가 서로 다른 범위의 outlier score를 반환할 경우, 이를 일정한 기준을 바탕으로 표준화시키는 작업, 즉 “score normalization” 이 필요하다. 예를 들어, 첫 번째 base detector $B_1$으로는 LOF (local outlier factor)가, $B_2$로는 GMM (gaussian mixture model)이 사용되었다고 가정해보자. 이 때, LOF가 반환하는 outlier score는 거리에 대한 척도로서, 그 값이 크면 클수록 이상치일 가능성이 높아진다. 반면에, GMM의 outlier score는 (log) likelihood 값으로, 그 값이 작은 엔트리들을 이상치로 판단한다. 이처럼 애당초 부호가 상반되는 경우 이외에도, LOF처럼 normalized된 outlier score값을 반환하는 알고리즘과 kNN처럼 스케일링이 되지 않은 outlier score 반환하는 알고리즘이 있기 때문에 다양한 base detector로 부터 얻어진 값들을 일정한 범위로 표준화 하는 작업은 성공적인 앙상블 학습을 위해 필수적이라고 할 수 있다.

이와 관련해서, 가장 일반적인 표준화 방법으로는 “Min-max scaling”과 “Z-transformation”이 있다.

Min-max scaling

$$ S_j(i) = \frac{s_j(i) - min_j}{max_j - min_j} $$

Z-transformation

$$ S_j(i) = \frac{s_j(i) - \mu_j}{\sigma_j} $$

두 방법간 우위를 직접적으로 비교할 수는 없으나, 일반적으로 후자가 조금 더 안정적인 스코어를 얻을 수 있다는 점에서 더 선호되는 것으로 보인다. 그 이유는 Min-max scaling의 경우 outlier score가 최대값과 최소값에 크게 의존할 수 밖에 없는데, “이상치”의 특징을 고려할 때 이러한 극단적인 값들은 수치적으로 상당히 불안정할 수 있기 때문이다. 이 밖에도 outlier score를 직접적인 확률값으로 변환시키려는 아이디어가 해당 논문에서 제안되었다.

2.2. Score Combination

한편, score normalization을 통해 각 base detector마다 통일된 범위 내의 outlier score를 얻었다면, 그 다음으로는 해당 값들을 어떻게 하나의 지표로 압축할지에 대한 논의가 필요하다. 이러한 맥락에서 고려해볼 수 있는 접근법은 크게 “평균”, “최대값”, “순위”를 이용하는 것이다.

Score Averaging
$$ \text{Score}(i) = \frac{\sum_{j=1}^m S_j(i)}{m} $$
- 이 경우, 최종적인 outlier score는 개별적인 base detector에서의 스코어를 평균낸 것으로 정의된다.
- 이는 통계적으로 더 낮은 분산을 갖는 outlier score를 얻을 수 있다는 장점이 있다.
Score Maximization
$$ \text{Score}(i) = \text{max}_{j=1}^m S_j(i) $$
- 이 경우, 최종적인 outlier score는 개별적인 base detector에서의 최대값으로 정의된다.
- 이는 각 base detector마다 특화된 이상치들이 있을 것이라는 가정을 전제로 하는데, 따라서 base detector의 개별적인 성능이 상당히 중요해진다.
- 최대값은 특정한 base detector에서만 발견될 수 있는 까다로운 이상치들을 탐지하는데 효과적일 수 있으나, 이상치의 특성상 이는 outlier score의 분산을 증가시켜 다소 안정성이 떨어질 수 있다는 우려가 있다.
- 이와 관련해서 안정성을 증가시키기 위해 AOM method 등이 제안되었다 (p. 216 참고).
Label Averaging
$$ \text{Score}(i) = \frac{\sum_{j=1}^m O_j(i)}{m}, \quad O_j(i) = \begin{cases} \mbox{1,} & \mbox{if } S_j(i) > \text{threshold} \\ \mbox{0,} & \mbox{otherwise} \end{cases} $$
- 이 경우, $i$ 번째 데이터 포인트에 대한 base detector의 스코어들은 일정한 기준에 의해 정상이면 0, 이상치면 1의 값을 갖는 binary label $O_j(i)$로 우선적으로 변환된다.
- 이후 score averaging과 동일하게 해당 값들을 평균내어 최종적인 outlier score를 정의한다.
- 이러한 방법은 개별적인 base detector에서의 outlier score가 수치적으로 상당히 불안할 우려가 있는 경우 (e.g. likelihood) 효과적이며, 정상치들의 영향력을 감소시키는 효과가 있다.

3. Theoretical Foundations of Outlier Ensembles

다음으로는 개념적인 측면에서 이상치 탐지 과제에 앙상블 학습을 적용하는 것이 갖는 의의에 대해서 살펴보자. 즉 앙상블 학습이 도대체 왜 (일반적으로) 더 나은 결과를 보장하는지에 대한 단서를 찾아보고자 하는 것이다.

3.1. Bias-variance tradeoff in Supervised Analysis

이를 위해 우리는 분류, 클러스터링 등의 supervised data mining 분야에서 등장하는 개념인 “bias-variance tradeoff” 에 주목할 필요가 있다. 이에 대한 구체적인 설명은 이전의 포스트에서 다룬적이 있는데, 일반적인 데이터 마이닝의 맥락에서 “bias”는 학습에 사용된 데이터를 얼마나 잘 설명하는지를 판단하는 지표이며 (i.e. overfitting), “variance”는 해당 모형이 학습에 사용되지 않은 데이터에 대해 얼마나 잘 일반화되는지를 나타내는 지표라고 이해하면 편하다. 일반적으로 bias와 variance를 둘 다 감소시키는 것은 불가능한데 (tradeoff relationship), 이러한 맥락에서 학습된 모형은 타겟의 라벨값을 바탕으로 bias와 variance 간의 적절한 밸런스를 갖추도록 설계된다. 즉, bias를 최소화하기 위해 훈련용 데이터에 대해서 모형을 최적화하는 동시에, 학습에 사용되지 않은 테스트 데이터에서의 성능을 평가함으로서 variance를 낮추려고 하는 것이다.

이처럼 supervised task에서는 주어진 데이터의 “라벨”에 대한 정보를 적극적으로 활용해서 bias-variance의 최적화를 수행할 수 있다. 한편, 우리의 관심사인 이상치 탐지 과제에서는 이러한 식의 bias-variance에 대한 최적화가 불가능하다. 그 이유는 앞서 수차례 언급한 것처럼 이상치 탐지 과제의 본질이 비지도 학습 (unsupervised learning)을 기반으로 하기 때문이다. 이처럼 어떤 것이 이상치인지에 대한 라벨이 부재한 상황 속에서는 만들어진 이상치 탐지 모형에 대한 bias와 variance를 객관적으로 평가하는 것이 불가능해진다.

3.2. Bias-variance tradeoff in Outlier Analysis

한편, 그럼에도 불구하고 이상치 탐지에서도 “개념적으로” bias variance tradeoff 를 정의하는 것은 가능하다. 이제 이러한 이슈가 앙상블 기법과 어떠한 관련이 있는지에 대해서 파헤쳐보도록 하겠다.

모든 이상치 탐지 과제는 주어진 데이터의 정상적인 생성 과정 (generative process) 을 모델링한 모형을 바탕으로 수행된다. 이를 수식을 사용해서 정의하자면, 주어진 데이터 $D$ 에 대한 정상적인 생성 과정 $f(\cdot)$ 을 효과적으로 카피할 수 있는 모형 $g(\cdot)$ 를 만드는 것이다. 이 때 true model 인 $f(\cdot)$ 은 우리가 절대로 알 수 없는 이른바 “true oracle” 이다.

한편, 이 과정에서 모형의 성능을 평가하기 위한 총 $n$개의 테스트 데이터 $\bar X_1, \cdots, \bar X_n$가 있다고 “가정”해보자. 물론 비지도 학습의 특성상 이러한 테스트 데이터들은 실제로 관측되지 않는다. 그럼에도 불구하고 해당 값들이 “이론적으로는” 존재한다고 생각해 볼 수 있을 것이다. 이 때, 이러한 테스트 데이터에 대해서 true model인 $f(\cdot)$ 에서의 outlier score $f(\bar X_i)$ 와, 우리가 만들어낸 모형 $g(\cdot)$ 에서의 outlier score $g(\bar X_i \;; D)$ 를 고려해보자.

자, 이제 우리의 관심사는 $g(\bar X_i \; ; D)$ 가 $f(\bar X_i)$ 에 비해 얼마나 차이가 나는지를 파악하는 것이다. 이에 대한 지표로, 우리는 다음과 같이 MSE (mean squared error)를 정의할 수 있다.

$$ MSE = \frac{1}{n}\sum_{i=1}^n \Big( f(\bar X_i) - g(\bar X_i \; ; D) \Big)^2 $$

한편, 여기서 주의해야 할 점은 바로 위 MSE는 “특정한 데이터셋” $D$ 에 대한 값이라는 점이다. 모형의 학습에 사용된 $D$ 는 $f(\cdot)$ 라는 generative process로부터 생성 (realized) 된 $N$개의 데이터 포인트의 집합인데, 이 때 만약 $f(\cdot)$ 으로 부터 $N$개의 데이터를 추출하는 과정을 여러번 반복할 경우 그 결과로 얻어지는 데이터셋은 $D_1, D_2, \dots, D_\infty$ 과 같이 여러개의 replication을 가질 것이다. 이처럼 $D$ 는 오직 특정한 한 시점의 정보량만을 담고 있기 때문에, 이상치 탐지 모형의 성능에 대한 객관적인 평가를 위해서는 데이터셋에 대한 서로 다른 replication $D_1, \dots, D_k$ 에서의 평균적인 MSE 값을 계산해야만 한다.

$$ \begin{aligned} \mathbb{E}\big[ MSE \big] &= \frac{1}{n}\sum_{i=1}^n \mathbb{E}\Big[ \Big( f(\bar X_i) - g(\bar X_i \; ; D) \Big)^2 \Big] \\[15pt] &= \quad \cdots \\[15pt] &= \frac{1}{n} \sum_{i=1}^n \Big( f(\bar X_i) - \mathbb{E}\big[ g(\bar X_i \;; D) \big] \Big)^2 + \frac{1}{n} \sum_{i=1}^n \mathbb{E}\Big[ \Big( \mathbb{E}\big[g(\bar X_i \;; D)\big] - g(\bar X_i \;; D) \Big)^2 \Big] \\[15pt] &= \text{Bias}^2 + \text{Variance} \quad\quad\quad \cdots (A) \end{aligned} $$

위 식의 구체적인 유도 과정은 텍스트북의 p.194에 자세하게 나와있다. 여기서 중요한 점은 결론적으로 MSE의 평균값이 bias와 variance로 쪼개진다는 점이다.

이제 앙상블 기법이 개념적으로 어떤 효과를 갖는지를 이해하기 위한 모든 준비가 끝났다. 결국 우리의 궁극적인 목표는 true model $f(\cdot)$에 대해 $\mathbb{E}[MSE]$의 값을 최소화하는 모형 $g(\cdot)$ 을 찾고 싶은 것이다. 그리고 $(A)$를 통해서 알 수 있는 것은 $\mathbb{E}[MSE]$ 의 값을 줄이기 위해서는 모형의 bias와 variance 각각을 감소시키면 된다는 사실이다. 이러한 맥락에서 “outlier ensemble” 이란 그 목적에 따라 variance를 감소시키기 위한 “variance-reduction ensemble”과, bias를 감소시키기 위한 “bias-reduction ensemble”의 두가지로 구분될 수 있다. 각각에 대해서 하나씩 살펴보자.

4. Variance-reduction ensembles

앞서, 이상치 탐지에서 “variance”란 학습에 사용되지 않은 데이터셋에서 모형이 성능이 얼마나 일반화될 수 있는지를 평가하기 위한 지표라는 점을 살펴보았다. 이러한 맥락에서 “variance reduction ensemble”은 독립적인 학습 과정을 통해 얻어진 여러개의 결과를 하나로 수합해 이상치를 판단하려는 앙상블 기법을 의미한다. 이는 우리가 일반적으로 생각하는 형태의 앙상블로, 앞서 살펴본 model-centric ensemble과 data-centric ensemble 전부를 포함한다. 이처럼 여러개의 모형으로부터 발생한 randomness는 일반적으로 variance를 감소시키는 효과가 있음이 연구되었다 (참고).

구체적인 예시를 바탕으로 앙상블의 효과를 파악해보자. 아래의 그림은 서로 다른 3개의 독립적인 알고리즘 A, B, C 에 대해서 각 200번의 randomized training을 수행한 다음, 그 결과인 ROC-AUC를 상자 그림으로 나타낸 것이다. 이를 통해 우리는 앙상블의 결과가 독립적인 시행들의 평균값보다 더 높다는 점을 알 수 있는데, 이 과정에서 개별적인 성능의 편차가 큰 알고리즘 C와 같은 경우에서 앙상블 학습은 더욱 큰 효과를 발휘할 수 있다는 점이 일반적으로 알려져있다.

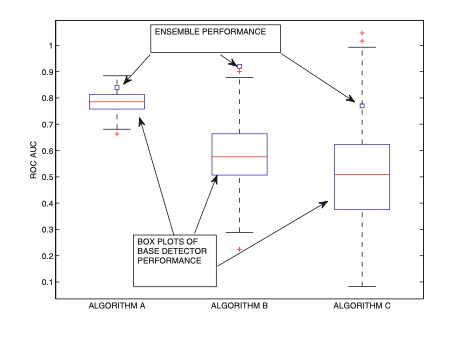
Figure 1. Example of base detector (box plot) and ensemble (square marker) performances for base detectors with varying levels of stability.

4.1. Parametric Ensembles

이러한 맥락에서 가장 대표적인 variance reduction ensemble 기법은 바로 특정한 (모수적) 모형에 대해 여러 하이퍼파라미터 셋팅 아래에서의 결과를 앙상블하는 것이다. 가령, kNN 알고리즘에 parametric ensemble을 적용할 경우, 가장 중요한 하이퍼 파라미터라고 할 수 있는 클러스터의 개수 $k$ 에 대한 앙상블을 고려해볼 수 있다. 즉, 데이터셋의 크기를 고려해 합리적인 $k$의 범위를 설정한 다음, 해당 범위 내의 랜덤하게 값을 바탕으로 모형을 학습시킨다. 그리고 최종적인 이상치의 판단은 해당 결과들로부터 얻어진 결과에 평균을 취하는 것으로 이뤄진다.

이러한 앙상블 기법은 supervised algorithm처럼 라벨에 대한 정보를 바탕으로 그리드 서치 등을 통해 최적의 하이퍼파라미터를 찾는 것이 불가능한 상황에서, 모형의 모수로부터 발생하는 불확실성 (i.e. variance)를 줄이는데 효과적으로 사용될 수 있다. 이와 같은 parametric ensemble에 대한 pseudo-algorithm은 다음과 같다.

Figure 2. Pseudo-algorithm of parametric ensembles

이와 더불어 kNN이나 EM 기반의 GMM 등 알고리즘의 시작점 (initialization point)이 결과에 영향을 미치는 방법론들에 대해서는 임의로 여러개의 시작점을 선택한 다음 해당 결과들을 하나로 수합하는 앙상블을 활용하는 것이 효과적일 것이다. 이러한 전략을 “randomized detector averaging” 이라고 부르는데, 주로 클러스터링 또는 밀도 추정을 활용하는 방법론들에 자연스레 적용해볼 수 있다.

4.2. Feature Bagging

앞서 고차원에서의 이상치 탐지와 관련해서 간단하게 살펴본 바 있는 “Feature Bagging”을 앙상블 기법의 관점에서 다시 한번 살펴보도록 하자.

해당 방법론의 핵심적인 아이디어는 데이터셋을 구성하는 $d$ 차원의 feature space에서 임의로 $r$ 개의 축 (axis)을 선택한 다음, 해당 축들로 이루어진 부분 공간에 데이터를 투영시켜 이를 바탕으로 이상치 탐지 알고리즘을 적용시키려는 것이다. 이후 이러한 부분 공간들에서의 결과를 maximization, 또는 averaging하는 것을 통해 최종적으로 이상치를 판단하게 된다.

이처럼 feature bagging은 유한한 데이터로부터 발생하는 model variance를 낮춰준다는 점에서 variance-reduction ensemble의 한 종류라고 할 수 있다. 그리고 이 과정에서 더 낮은 차원의 부분 공간을 사용하면 사용할 수록 variance의 감소폭이 더 커지게 된다. 허나 이는 반대로 차원 축소로 인해 줄어든 정보량으로 인해 bias를 증가시키는 tradeoff가 있는데, 따라서 feature bagging에서 차원수 $r$ 은 꽤나 중요한 파라미터라고 할 수 있다. 이와 관련해서 일반적으로는 $r$ 을 일정한 범위에서 랜덤하게 선택하는 방법이 활용된다. Feature bagging에 대한 pseudo-algorithm은 다음과 같다.

Figure 3. Feature Bagging

한편, feature bagging의 한가지 약점은 충분한 차원 수가 보장되어야 한다는 점이다. 가령, 6차원의 데이터셋에 feature bagging을 적용한다고 해보자. 이 경우 가능한 저차원 공간의 모든 조합에 대해서 3차원은 $6 \choose 3 $ $= 20$ , 4차원은 15, 5차원은 6개의 가능성이 존재한다. 결과적으로 해당 데이터셋에서는 feature bagging을 적용하는 과정에서 앙상블의 개수가 늘어나면 늘어날수록 3차원의 영향력이 다른 차원들에 비해 상대적으로 커지게 되는 문제가 발생한다. 이처럼 충분한 차원수가 보장되지 않거나, 혹은 base detector 간의 상관 관계가 큰 경우 feature bagging은 의도했던 만큼의 variance reduction을 보장하지 못할 수도 있다. 이러한 feature bagging의 문제점을 해결할 수 있는 한가지 대안은 임의의 회전 축 (rotation axis)을 바탕으로 부분 공간 탐색을 수행하는 “rotated bagging” 이다 (이전 포스트 참고).

4.3. Data-Centric Variance Reduction with Sampling

“Data-centric” variance reduction의 핵심적인 가정 사항은 우리가 현재 갖고 있는 데이터가 더 큰 모집단으로부터 발생된 랜덤 샘플이라고 파악하는 것이다. 따라서 주어진 데이터를 바탕으로 수행된 이상치 탐지의 결과는 동일한 모집단으로부터 생성된 다른 데이터에 대해 수행된 이상치 탐지의 결과와 비교했을 때 다소 차이가 발생할 수 밖에 없는데, 바로 이 부분이 variance를 발생시키는 원인이 된다. 이러한 맥락에서 앙상블의 목표는 주어진 (유한한) 데이터를 최대한 잘 활용해서 variance를 최소화하려는 시도이다.

그렇다면 주어진 데이터를 가장 잘 활용하는 방법은 과연 무엇일까? 가장 간단한 방법은 샘플링을 이용해서 주어진 데이터로부터 여러개의 복제본 (replication)을 만드는 것이다. 그 대표적인 방법으로는 bagging과 subsampling이 있는데, 이를 통해 학습된 모형의 variance을 줄일 수 있다는 사실은 이론적으로 증명이 된 부분이다 (참고).

Bagging

자 그렇다면 우선 “bagging”에 대해서 살펴보자. Bagging이란, 주어진 $N \times d$ 데이터셋 $D$ 에 대해서 복원 추출을 바탕으로 동일한 크기를 갖는 복제 데이터 $D^{(*)}$ 를 정의하는 것이며, 이러한 아이디어는 통계학에서 “부트스트래핑 (bootstrapping)” 이라고 불리기도 한다. 이는 우리에게 주어진 데이터가 모집단의 생성 매커니즘을 잘 대변한다는 전제를 바탕으로 한다. Bagging의 한가지 장점은 동일한 데이터가 $D^{(*)}$ 에 여러번 반복해서 포함될 수 있기 때문에, 이상치와 같이 generative probability가 상대적으로 낮은 값들의 영향력이 줄어들어 데이터 자체의 노이즈가 줄어들 수 있다는 점이다. 한편, bagging의 대표적인 단점은 복원 추출로 인해 데이터 간의 독립성이 보장되지 않는다는 점과, 만약 주어진 데이터가 모집단을 제대로 대표하지 못할 경우 bias를 증가시켜 오히려 전체적으로 모형의 성능을 악화시킬 가능성이 있다는 점이다.

Variable subsampling

Bagging과는 아주 약간 다르게, “subsampling”은 주어진 데이터로부터 비복원 추출을 통해 복제 데이터를 정의하려는 것을 의미한다. 이렇게 정의된 복제 데이터를 바탕으로 모형을 학습시킨 다음, 전체 데이터셋에 대해서 그 성능을 평가한다. 단, 이 과정에서 학습에 사용된 데이터가 성능 평가에 재사용되기 때문에 어느 정도의 과대 적합 (overfitting)이 발생할 가능성이 있다. 따라서 과대 적합에 민감한 모형의 경우 (e.g. 거리 기반 알고리즘) 추출될 데이터의 크기를 일정한 수준으로 제한하는 등의 추가적인 조치가 필요하다. 가령, kNN 알고리즘의 경우 클러스터의 개수 $k$ 는 훈련 샘플의 크기에 상당히 민감한 하이퍼파라미터이다. 이 때 $N=1000$ 의 데이터에서 최적의 성능을 보인 $k=10$ 이, $N=10000$ 에서도 최적의 하이퍼파라미터라고 단언할 수는 없을 것이다.

이와 관련해서, “variable subsampling” 이라는 기법은 추출되는 데이터의 크기를 항상 일정한 범위로 고정시키는 것을 의미한다. 예를 들어, 샘플 사이즈를 $[n_1, n_2]$ 사이로 제한하는 variable subsampling은 다음과 같이 정의된다.

$\text{Uniform}\Big( \text{min}(1, \frac{n_1}{N}), \; \text{min}(1, \frac{n_2}{N}) \Big)$으로 부터 랜덤한 난수값 $f$를 생성한다. ($N$은 전체 데이터 사이즈)
오리지널 데이터로부터 $\lceil f \cdot N \rceil$ 개의 엔트리들을 랜덤하게 비복원 추출해서 복제 데이터 $D^{(*)}$를 정의한 다음, 이를 바탕으로 모형을 학습시킨다.
1 - 2를 앙상블의 개수만큼 반복한 뒤 결과를 앙상블한다.

단, 이 과정에서 한가지 주의해야 할 점은 각각의 복제 데이터로부터 얻어진 outlier score를 통일된 범위로 스케일링해야 한다는 점이다. 그 이유는 모형의 학습에 사용된 훈련 데이터의 크기가 앙상블마다 랜덤하게 정의되어 outlier score의 스케일이 서로 다르기 때문이다.

이러한 variable subsampling의 장점은 유한한 데이터로부터 발생하는 bias를 모형 내부적으로 훈련 데이터를 재정의하는 subsampling을 포함하는 것을 통해 variance의 요소로 치환한다는 점이다. 그리고 이렇게 발생한 model variance는 앞서 살펴본 것처럼 앙상블을 통해서 감소시킬 수 있다. 또한 $n_1$, $n_2$ 가 $N$ 에 비해 충분히 작을 경우, 각 앙상블에서 활용된 학습 데이터는 서로 상관 관계가 낮을 것이라는 점에서 독립적인 학습기들을 통한 앙상블의 효과를 극대화할 수 있다.

한편, 이처럼 오리지널 데이터의 일부분을 바탕으로 여러개의 병렬적인 학습을 진행하는 것은 앙상블의 한가지 구성 요소로서 다른 기법들과 함께 사용될 경우 더 나은 결과를 얻을 수 있다. 가령, 앞서 살펴본 rotated bagging을 variable subsampling과 함께 활용하는 것을 고려해 볼 수 있다. 이와 같이 전체 크기의 데이터셋에 특정한 base detector를 단 한번 학습시키는 것보다 데이터의 여러 부분 집합에 대해 앙상블을 적용하는 것은 컴퓨팅 속도를 포함한 성능의 측면에서 상당히 효과적일 수 있다.

5. Bias-reduction ensembles

Bias는 특정한 모형의 고유하게 내제된 “오류”를 의미하며, 이는 우리가 사용한 모형의 가정 사항이 실제 데이터에 잘 들어맞지 않기 때문에 발생한다. 따라서 “bias-reduction” 이란 학습시킨 모형 자체의 오차를 감소시키려는 시도를 나타낸다.

일반적으로 비지도 학습을 기반으로 수행되는 이상치 탐지 과제에서 모형의 bias를 줄이는 것은 variance reduction에 비해 상대적으로 훨씬 어려운 작업이다. 왜냐하면 이는 결과에 대한 정보 (라벨)가 없는 상황에서 주어진 단 하나의 데이터로부터 해당 데이터를 발생시킨 true generative process $f(\cdot)$ 를 추론하는 것으로, 문제를 풀기 위한 필요충분조건이 갖춰지지 않았기 때문이다. 이러한 맥락에서 이상치 탐지에서의 bias-reduction 테크닉들은 태생적인 한계점을 갖고 있다고 할 수 있다.

한편, 그럼에도 불구하고 개념적으로는 bias-variance tradeoff를 정의할 수 있다는 점을 앞서 식 $(A)$ 를 통해 살펴보았다. 이러한 맥락에서 비록 완벽하진 않지만 bias reduction을 위해 사용될 수 있는 휴리스틱적인 접근법 몇가지가 존재한다.

5.1. Data-Centric Pruning

결과적으로 이상치 탐지에서 bias-variance tradeoff 와 관련한 이슈가 발생하는 근본적인 원인은 라벨값의 부재 때문이라고 할 수 있다. 따라서 가장 간단하게 생각해볼 수 있는 방법은 특정한 비지도 학습 모형의 결과로 얻어진 결과를 임시로 라벨에 대한 참 값으로 간주하여 사용하는 것이다. 물론 이렇게 될 경우 모형의 훈련과 평가가 서로 독립이 아니라는 점에서 순환 오류가 발생할 것임은 자명하다. 허나 충분한 주의를 기울일 경우, 이러한 순환 오류로부터 발생하는 bias를 효과적으로 컨트롤하면서 전체적인 모형의 bias를 줄일 수 있을 것이라는 아이디어가 여러 연구들에 의해 제안되었다.

이러한 맥락에서 “data-centric pruning”이란 주어진 데이터에서 명백한 이상치들을 제거하는 것을 통해 좀 더 정제된, 즉 “정상”인 데이터들을 바탕으로 이상치 탐지 모형을 학습시키려는 시도를 의미한다. 구체적으로, 주어진 데이터 $D$ 를 바탕으로 이상치 탐지 모형 $M$ 을 학습시킨 다음, 그 결과로 얻어진 이상치 $O$ 들을 $D$ 에서 제외시킨다. 이제 이렇게 얻어진 정제된 데이터 $D^{*} = D - O$ 를 사용해서 다시 이상치 탐지 모형 $M$ 을 학습시킨다. 이러한 절차를 충분히 많이 반복할 경우, 결과적으로 정상인 데이터들로만 학습된 모형 $M$ 을 얻을 수 있을 것이다.

단, 이 과정에서 주의해야 할 점은 이상치 셋 $O$ 를 정의하는 과정에서 충분히 보수적인 기준 (outlier threshold)를 사용해야 한다는 점인데, 이는 의도치 않게 정상인 데이터들이 pruning 되는 것을 방지하기 위함이다. 가령, 데이터가 근사적으로 정규분포를 따를 경우, 3-$\sigma$ method는 이론적으로 약 0.3%의 엔트리만을 이상치로 정의할 것이라는 점에서 충분히 보수적인 outlier pruning이라고 할 수 있다.

이러한 아이디어는 주어진 데이터를 정제하여 모형의 bias를 줄이려는 시도라는 점에서 “data-centric”한 접근법이라고 불린다. 이를 알고리즘으로 나타내면 다음과 같다.

Figure 4. Data-Centric Pruning via Iterative Outlier Removal

5.2. Model-Centric Pruning

앞서 살펴본 data-centric pruning이 주어진 데이터의 관점에서 bias를 줄이려는 시도였다면, “model-centric pruning” 이란 모형의 관점에서 bias를 줄이려는 시도라고 할 수 있다. 이에 대한 대표적인 예시는 해당 논문에서 제시한 $SELECT$ 방법인데, 그 핵심적인 아이디어는 앙상블에 활용된 여러개의 base detector 중 성능이 좋지 못한 모형들을 제외하여 더 나은 결과를 얻으려는 것이다. 이러한 절차를 간단하게 요약하면 다음과 같다.

각 base detector로 부터 얻은 outlier score를 표준화한다 (e.g. min-max scaling, z-transformation).
- $i$ 번째 엔트리의 $j$ 번째 모형에 대해 표준화 된 스코어를 $S(i,j)$ 라고 하자.
$i$ 번째 엔트리에 대한 outlier score를 하나로 수합한 다음, 해당 값을 pseudo-ground-truth 라고 상정한다.
- $a_i = \frac{\sum_{j=1}^m O(i,j)}{m}$
- 이 때 pseudo-ground-truth 값은 집합 $a = [a_1, \dots, a_N]$ 을 binary label로 변환한 값에 대응된다.
pseudo-ground-truth 값과 비슷한 결과를 낸 base detector만을 선별한다.
- 해당 스텝을 논문에서는 “selection step”이라고 표현했다.
- 여기서 “비슷함”에 대한 척도로는 상관 계수가 사용되며, 상관 계수가 높은 모형을 순차적으로 앙상블 컴포넌트로 추가하는 작업을 pseudo-ground-truth와의 상관 계수가 감소하지 않을 때까지 반복한다.
3에서 얻어진 base detector 만으로 앙상블을 구성해서 최종적인 outlier score를 계산한다.

6. Summary

이상치 탐지에서의 앙상블 기법에 대한 연구는 최근에 큰 관심을 받고 있다. 그 단편적인 이유로는 복잡한 데이터일수록 이상치와 정상치가 복잡한 관계를 갖고 섞여있기 때문에 특정한 하나의 모형을 통해 모든 이상치들을 정확히 탐지하는 것이 현실적으로 불가능해지기 때문이다. 이전 포스트에서 살펴보았던 국소적인 공간에 이상치가 분포해있는 고차원 데이터셋이 그 대표적인 예시라고 할 수 있는데, 이러한 데이터에서는 여러 부분 공간의 결과를 하나로 수합하는 것을 통해 일반적으로 더 나은 결과를 얻을 수 있다는 점은 이제는 익숙할 것이다.

이와 관련해서 해당 포스트에서는 앙상블 기법의 디자인과 그 결과를 어떻게 하나로 수합할 것인지와 관련해 다양한 전략들을 살펴보았다. 또한 이론적인 측면에서 지도 학습 도메인의 bias-variance tradeoff 의 개념을 바탕으로 앙상블 기법을 통해 더 강건한 결과를 얻을 수 있다는 점에 대해 살펴보았다. 구체적으로는 feature bagging, subsampling 등의 variance reduction ensemble과, 비지도 학습으로 인한 태생적인 한계점이 있는 bias reduction ensemble이 있었다.

Reference

Aggarwal, C. C. (2013). Outlier Analysis. Springer. ISBN: 978-1-4614-6396-2
C. C. Aggarwal and S. Sathe. Outlier Ensembles: An Introduction. Springer, 2017.
J. Gao and P.-N. Tan. Converting Outlier Scores from Outlier Detection Algorithms into Probability Estimates. ICDM Conference, 2006.
Z.-H. Zhou. Ensemble Methods: Foundations and Algorithms. Chapman and Hall/CRC Press, 2012.
C. C. Aggarwal and S. Sathe. Theoretical Foundations and Algorithms for Outlier Ensembles. ACM SIGKDD Explorations, 17(1), June 2015.
L. Brieman. Bagging Predictors. Machine Learning, 24: pp. 123–140, 1996.
S. Rayana and L. Akoglu. Less is More: Building Selective Anomaly Ensembles. ACM Transactions on Knowledge Disovery and Data Mining, 10(4), 42, 2016.

# outlier-analysis # ensemble-analysis

[Outlier Analysis] Outlier Ensembles

1. Categorization of Ensemble Methods